Regular cube surface tours
by Jan Kristian Haugland

Back to Regular polyhedron surface tours main page

Other polyhedra:   Tetrahedron   Octahedron   Dodecahedron   Icosahedron

Here is a collection of (presumably) all regular cube surface tours with at most 200 vertices. Each one is given a label according to the number of vertices.
The label links to a text file containing the tour presented like a Gauss code for knots, except that we are not specifying "over" and "under" crossings, and it also contains
the feasible values of a and b. Next to the label, there is one or more illustration(s) (one for each (a, b) pair). These are also clickable for a better view of each one.

One might suspect that the number of vertices of a regular cube surface tour with two different (a, b) pairs and no double edges must be either 3 times a triangular number, or 8 times a generalized pentagonal number.

Tours		Illustrations		Comments		Additional illustrations
0				No crossing points Same as Octahedron-0 and Icosahedron-0
3				Contains double edges Same as Octahedron-3 and Icosahedron-3
4				Contains double edges Same as Octahedron-4 and Icosahedron-4
8				Same as Icosahedron-8
9				Same as Octahedron-9C and Icosahedron-9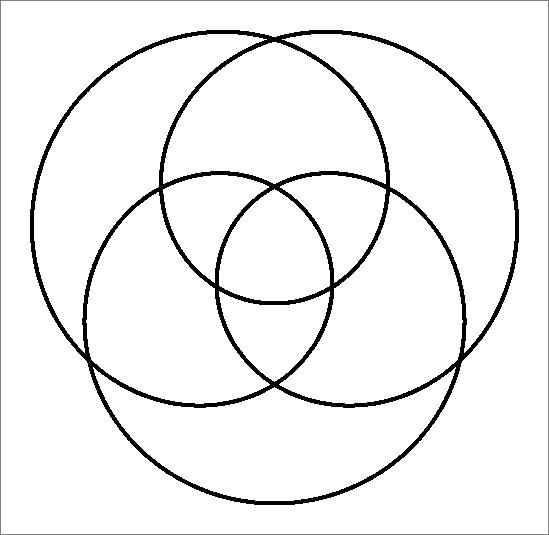
12A
12B				Contains double edges Same as Octahedron-12B and Icosahedron-12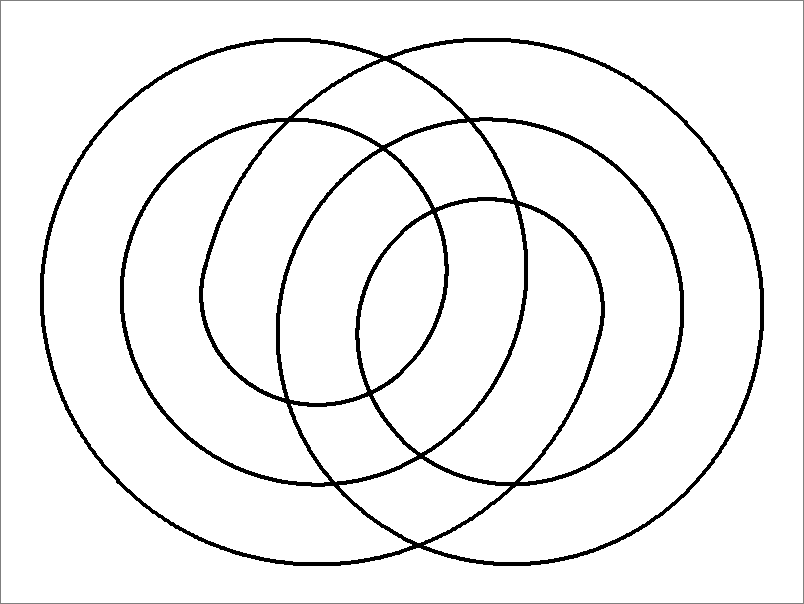
16				Same as Icosahedron-16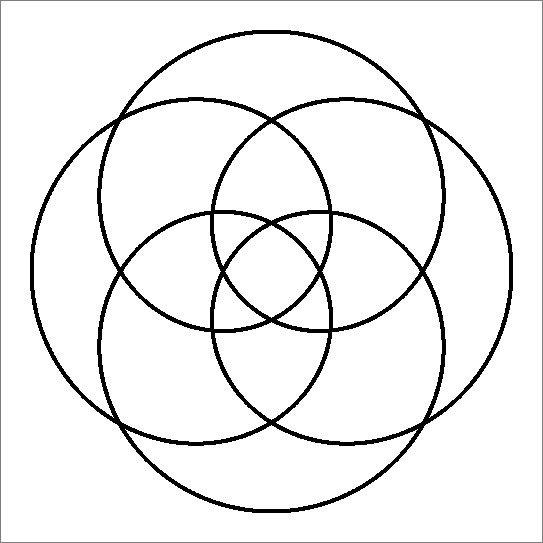
18				Same as Octahedron-18A and Icosahedron-18
20				Same as Icosahedron-20
24A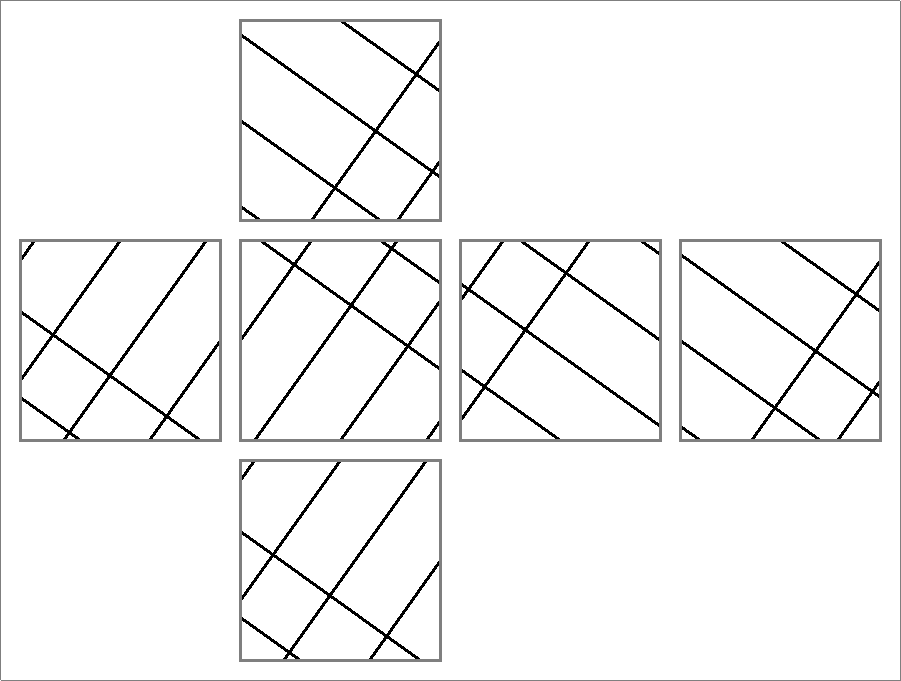
24B			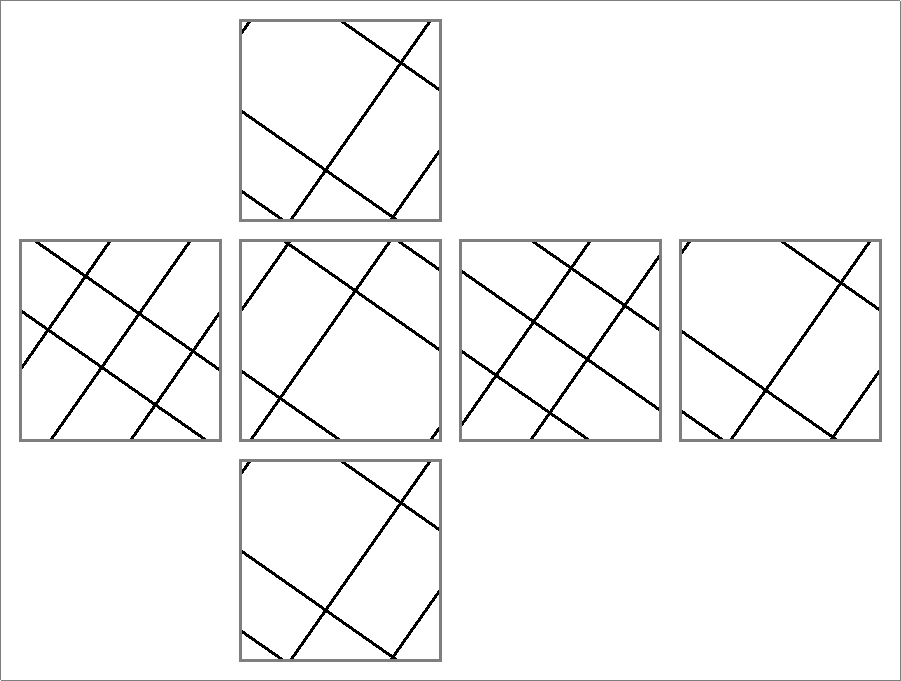	Same as Icosahedron-24B
24C			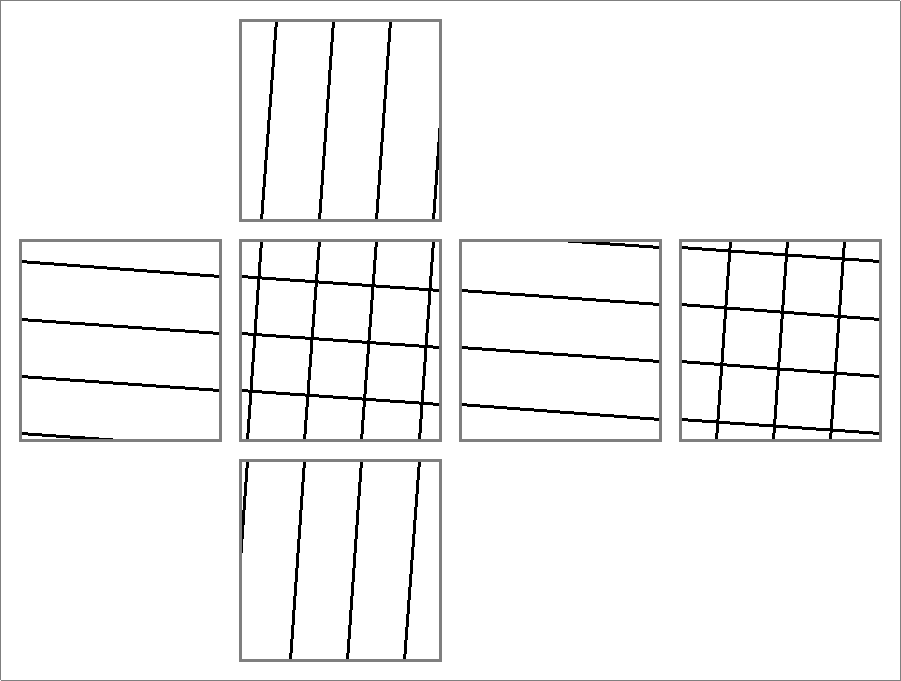	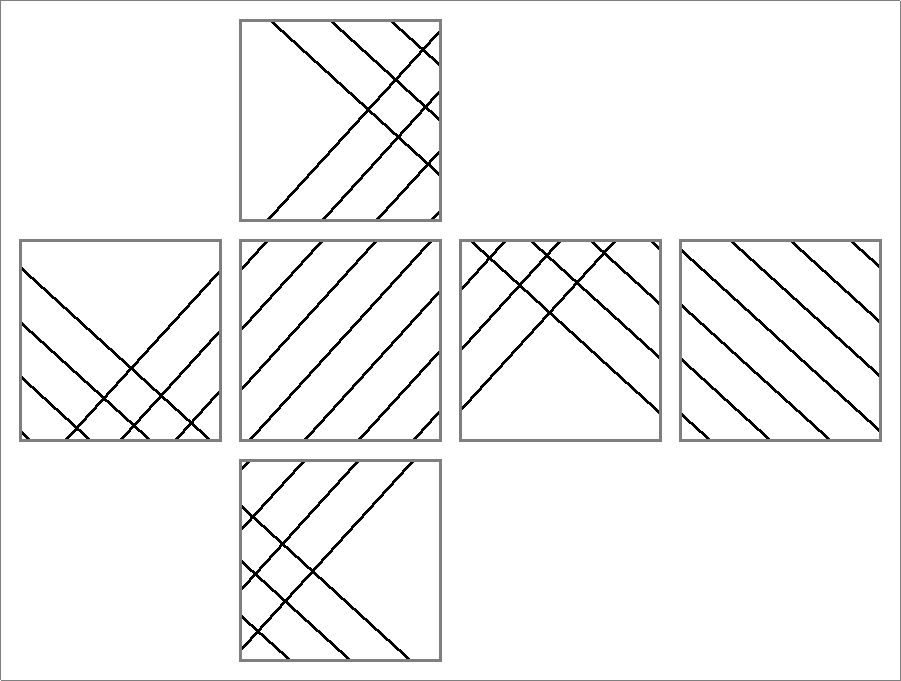Contains double edges Same as Octahedron-24B and Icosahedron-24C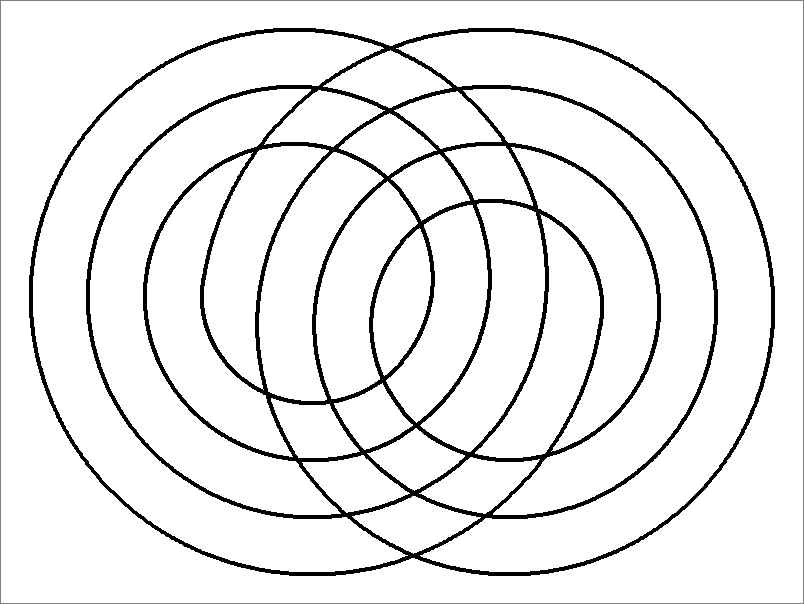
28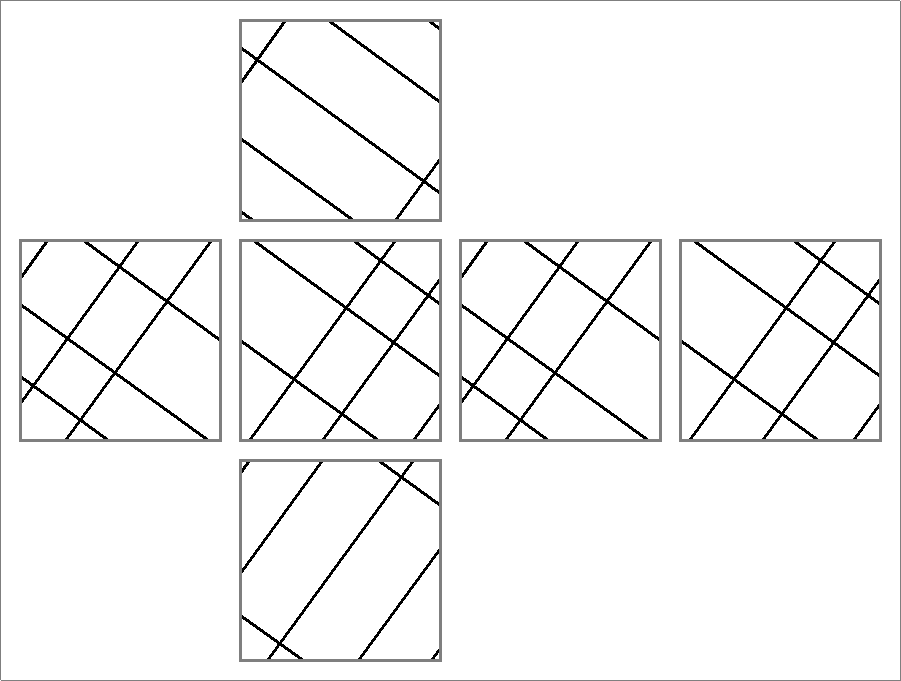
30			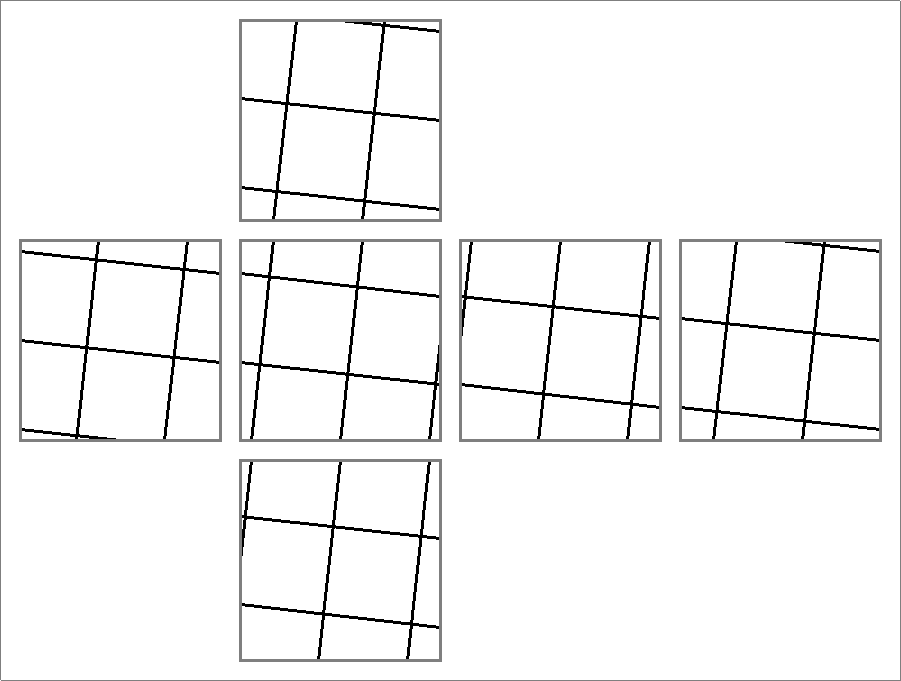	Same as Octahedron-30C and Icosahedron-30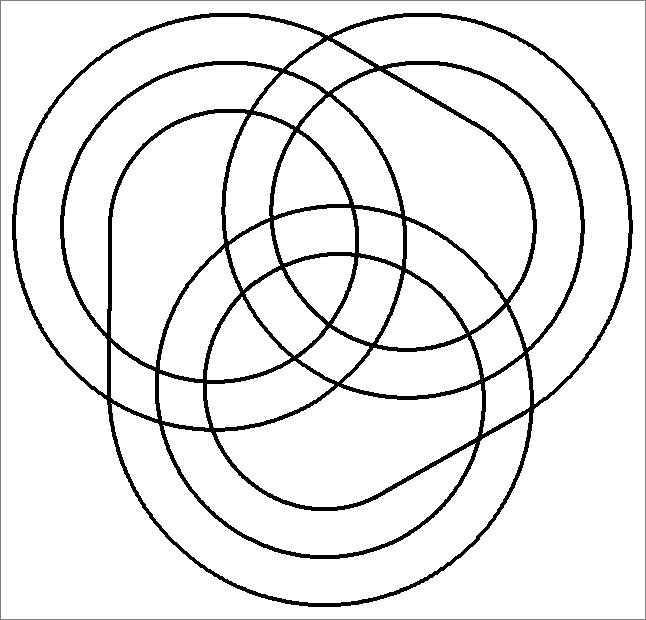
32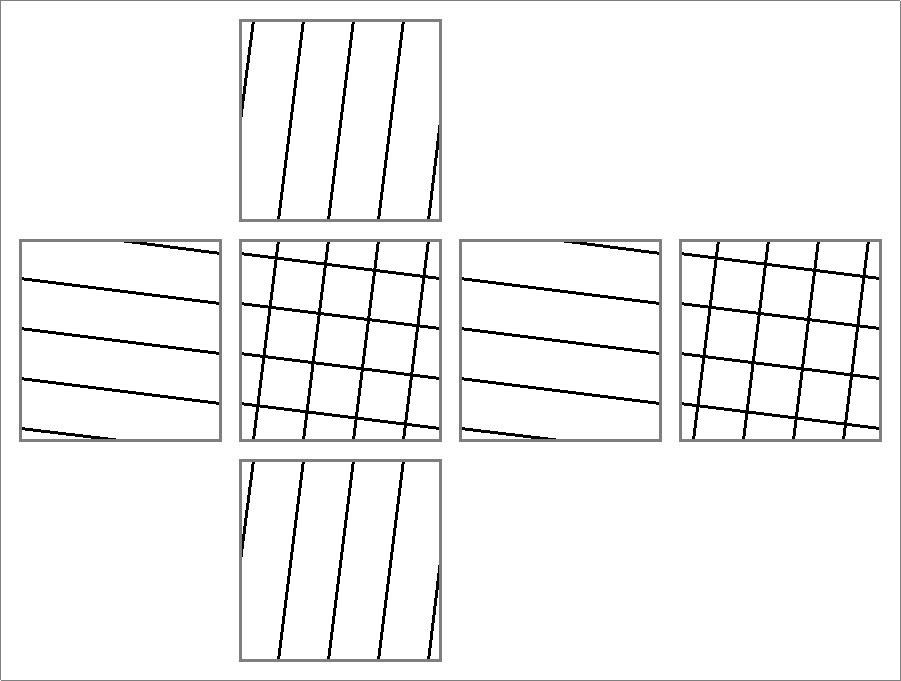
36A
36B			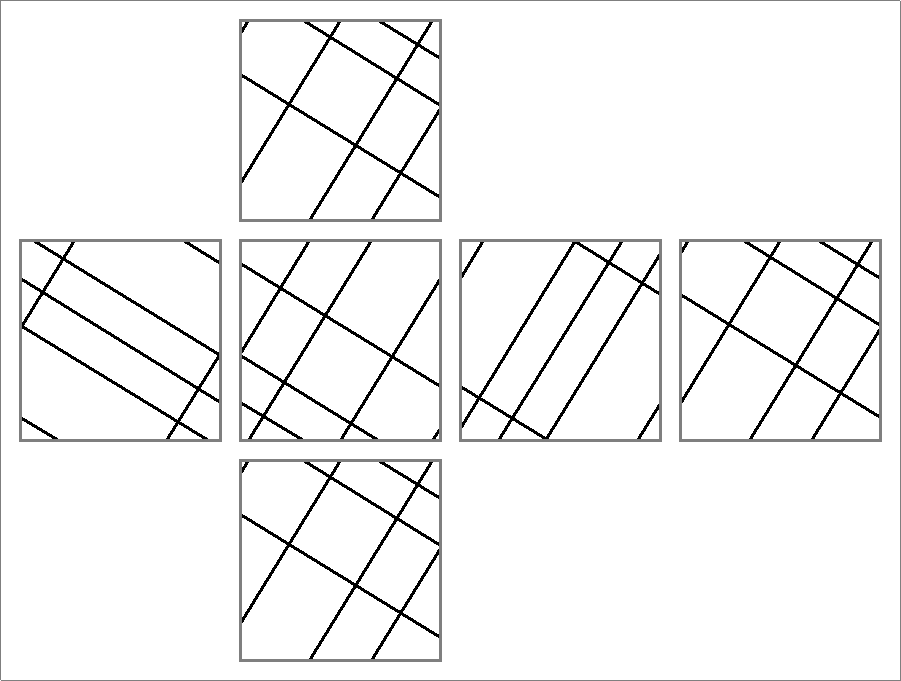	Same as Icosahedron-36
40A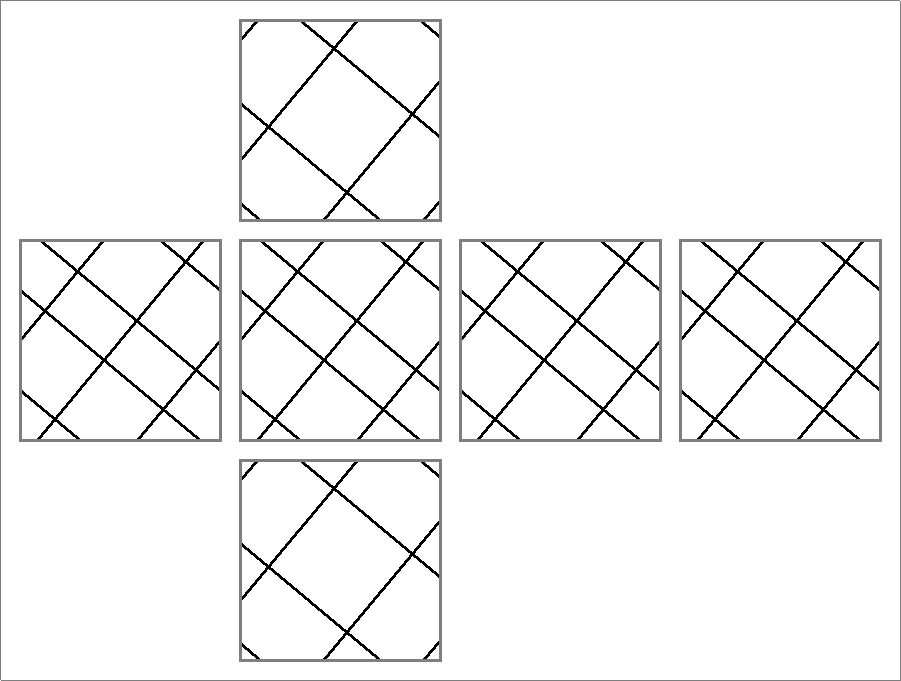
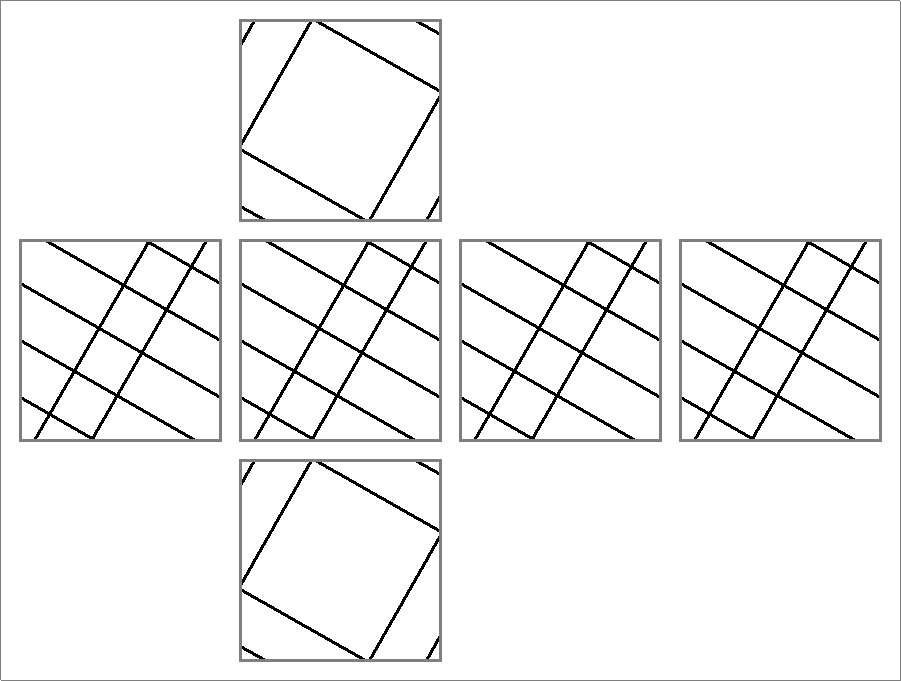40B				Contains double edges Same as Octahedron-40B and Icosahedron-40B
44A
44B				Same as Icosahedron-44
44C
45A				Same as Octahedron-45C and Icosahedron-45B
45B				Same as Icosahedron-45A
48A
48B
56A
56B
56C				Same as Icosahedron-56A
60A
60B			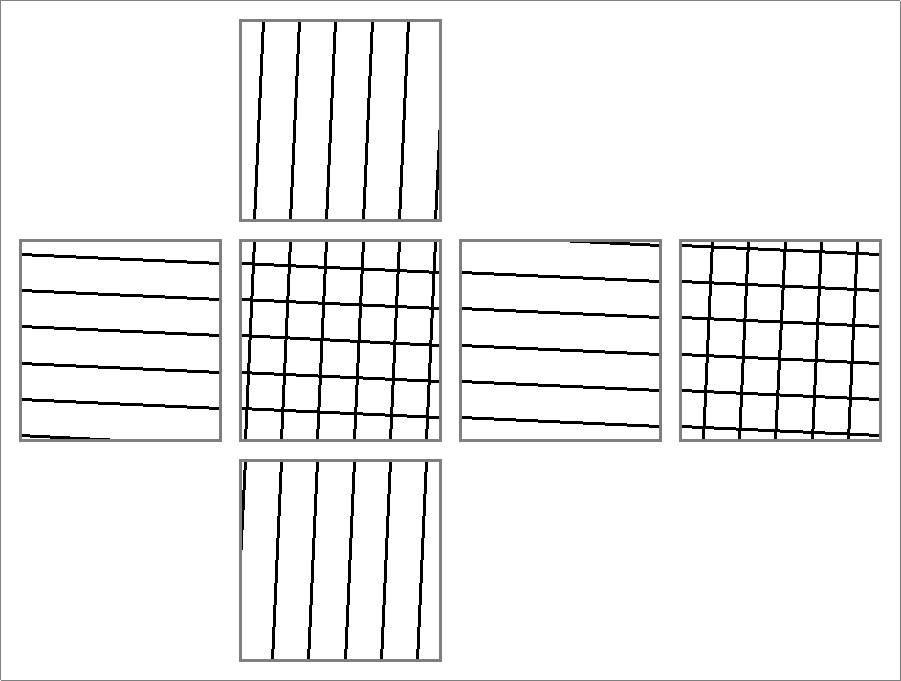	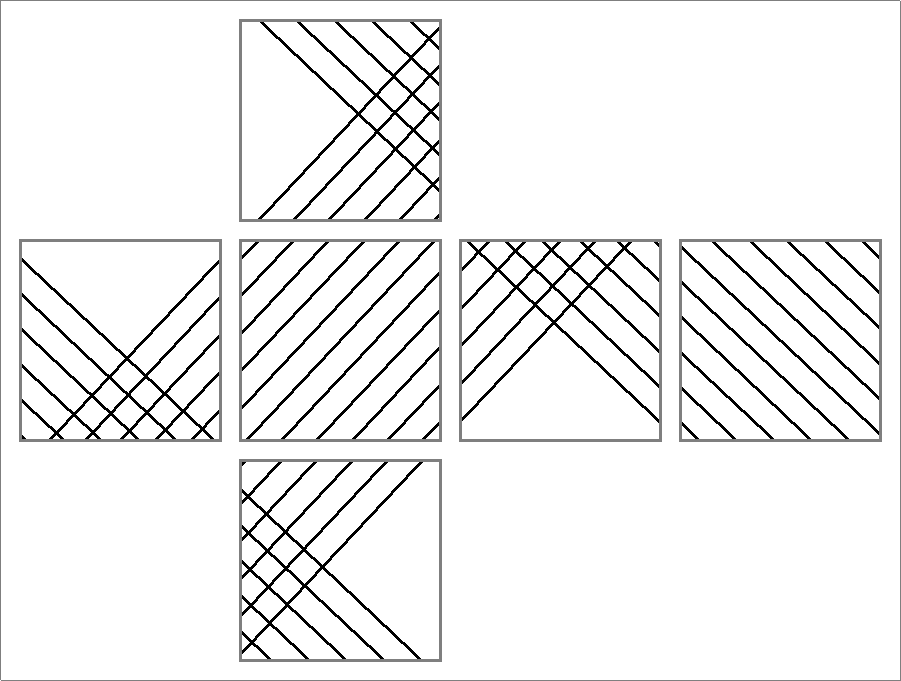Contains double edges Same as Octahedron-60C and Icosahedron-60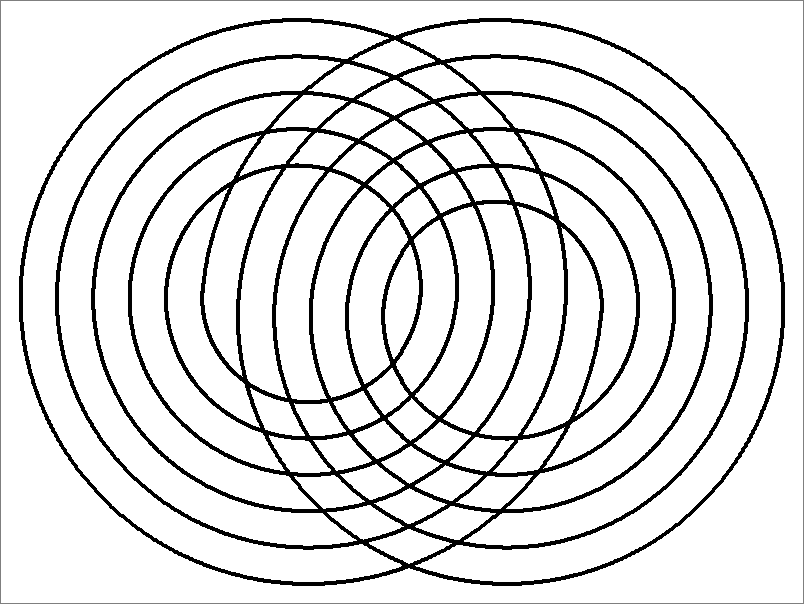
63A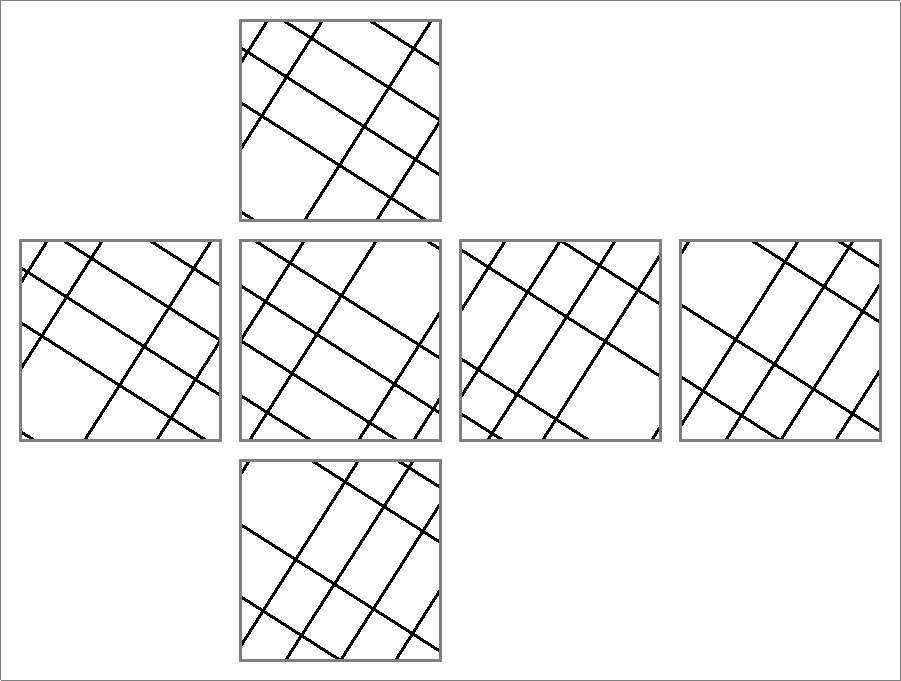
63B			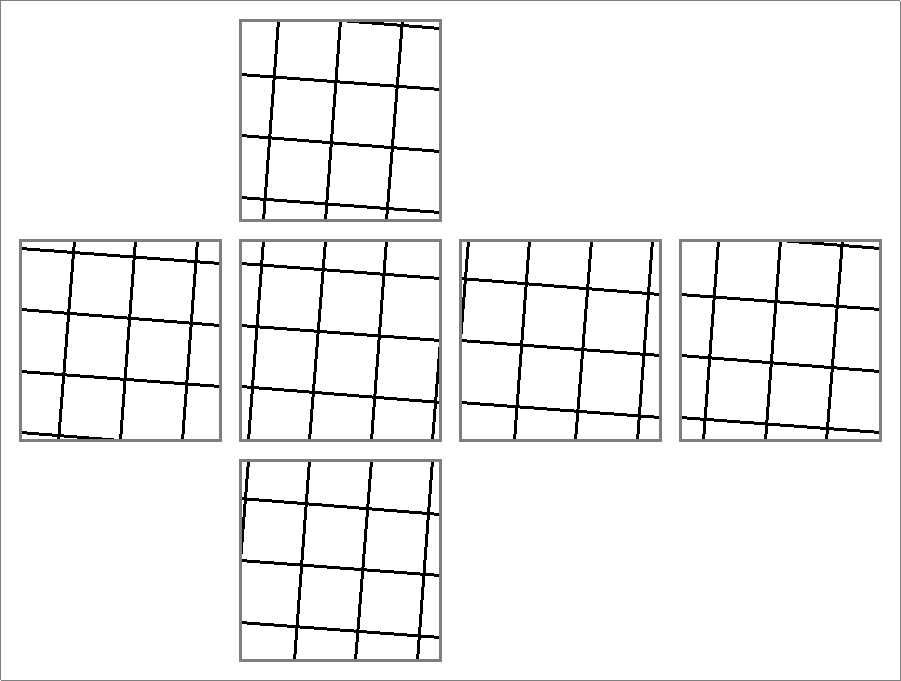	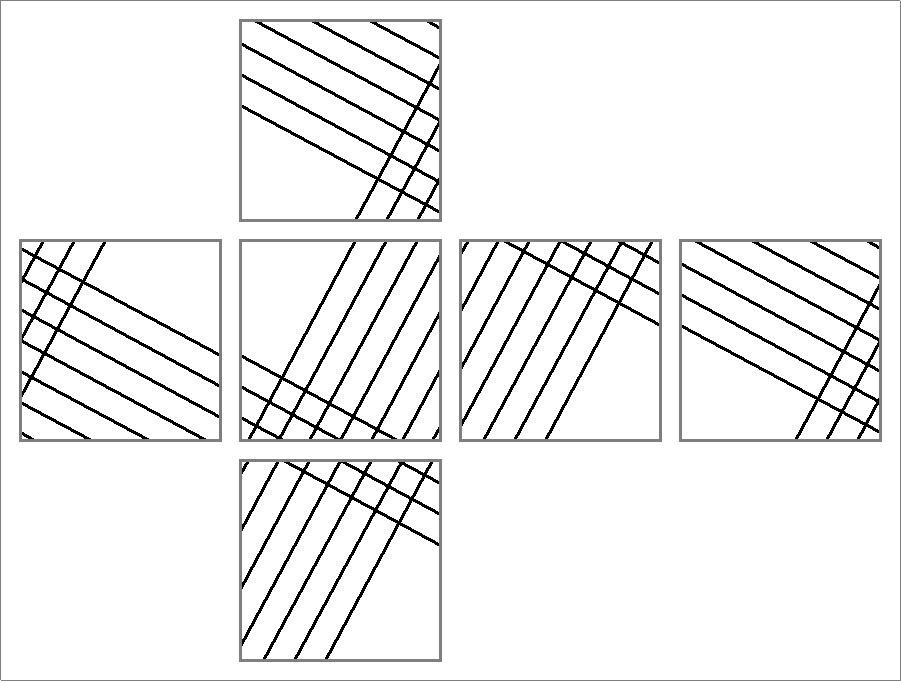Same as Octahedron-63C and Icosahedron-63C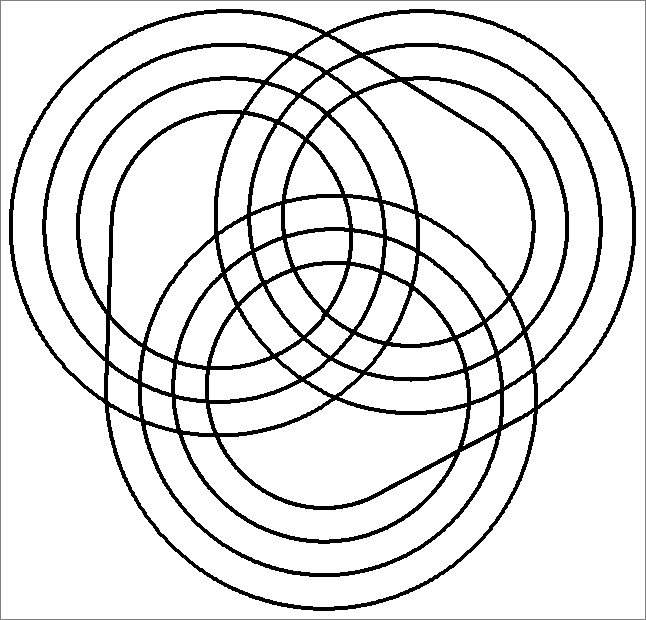
63C			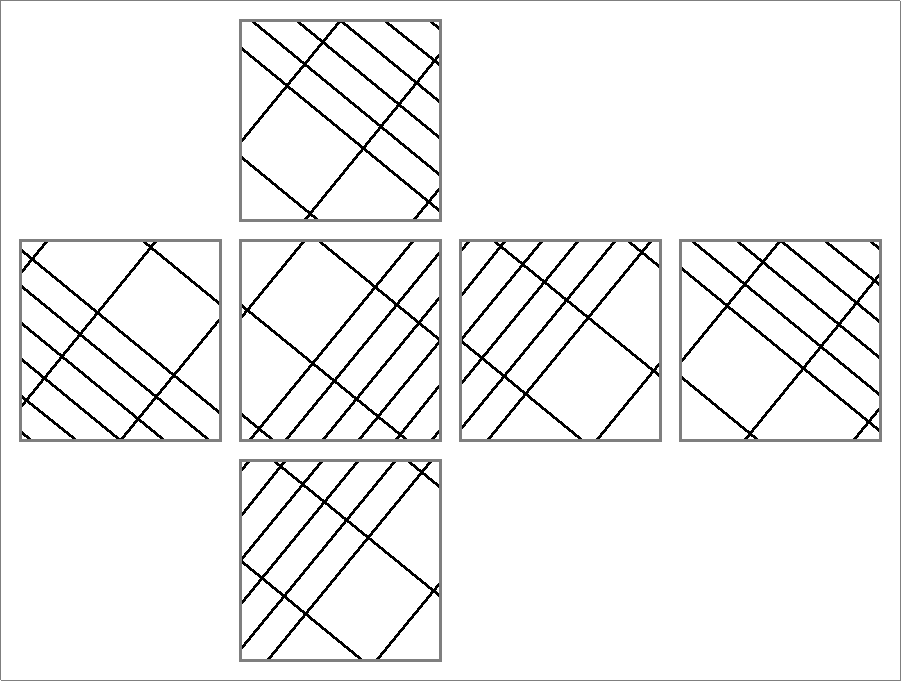	Same as Icosahedron-63B
66
68A				Same as Icosahedron-68A
68B				Same as Icosahedron-68B
69
72A
72B
72C
80A
80B
80C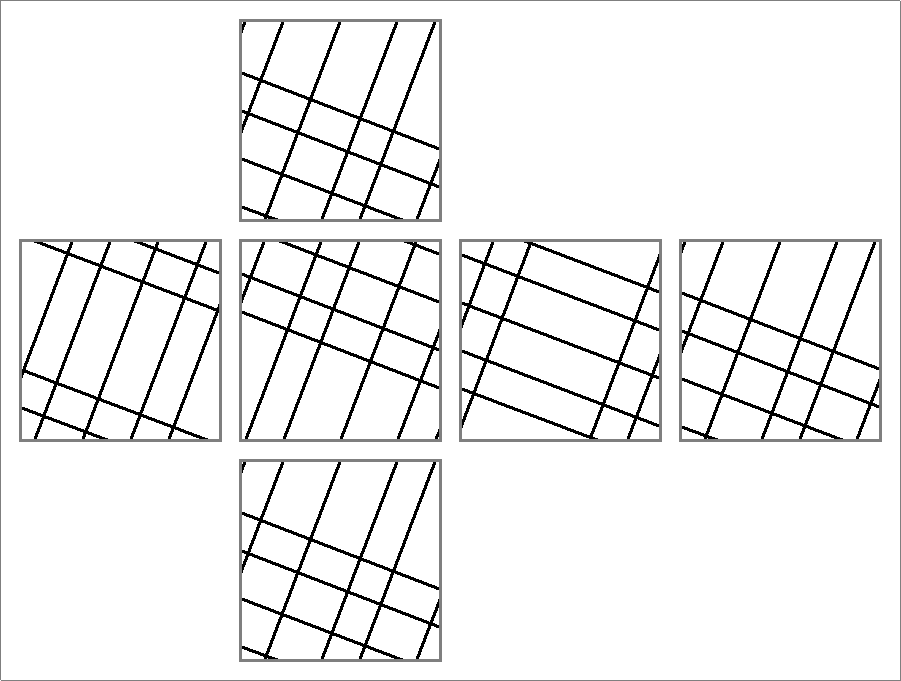
84A			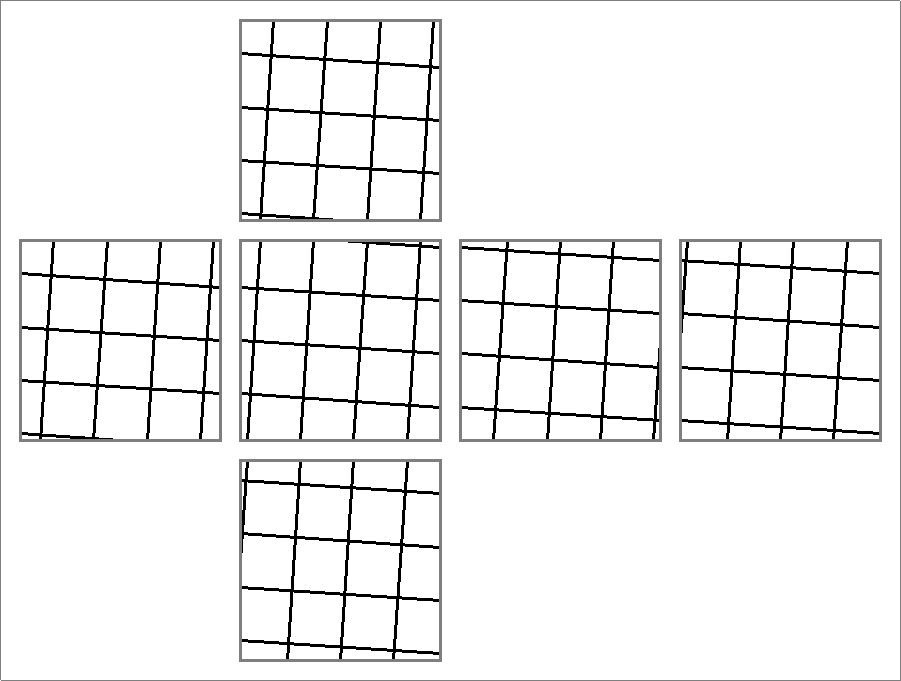	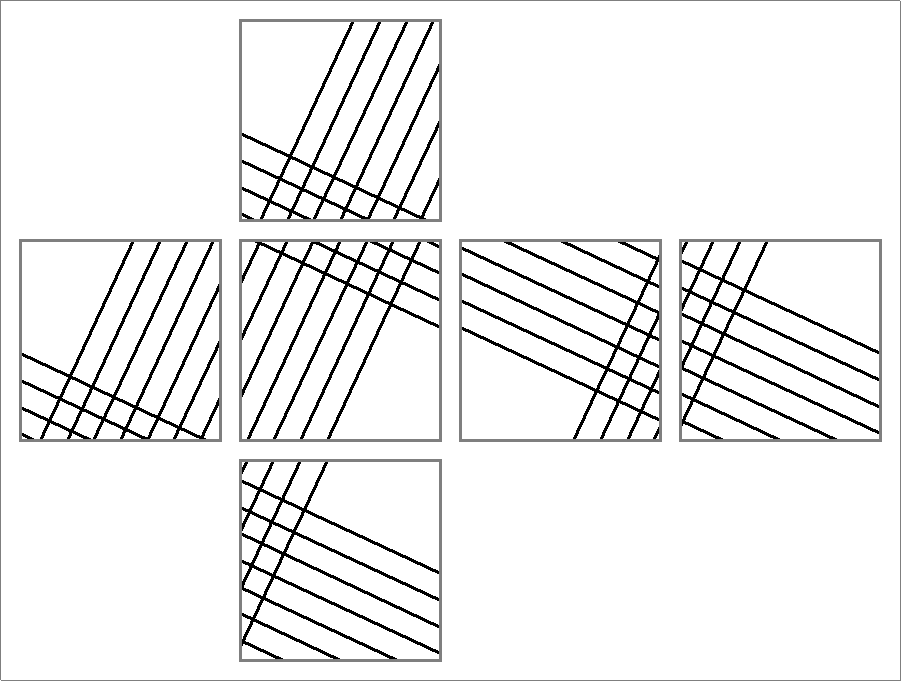Same as Octahedron-84A and Icosahedron-84A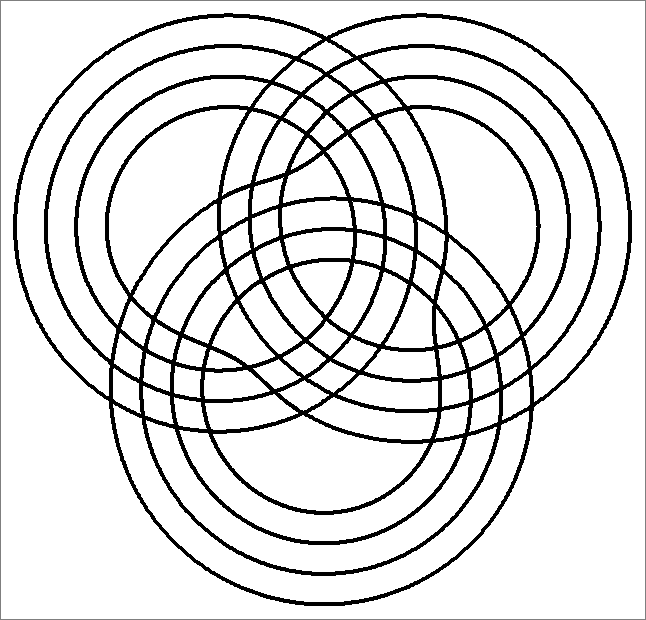
84B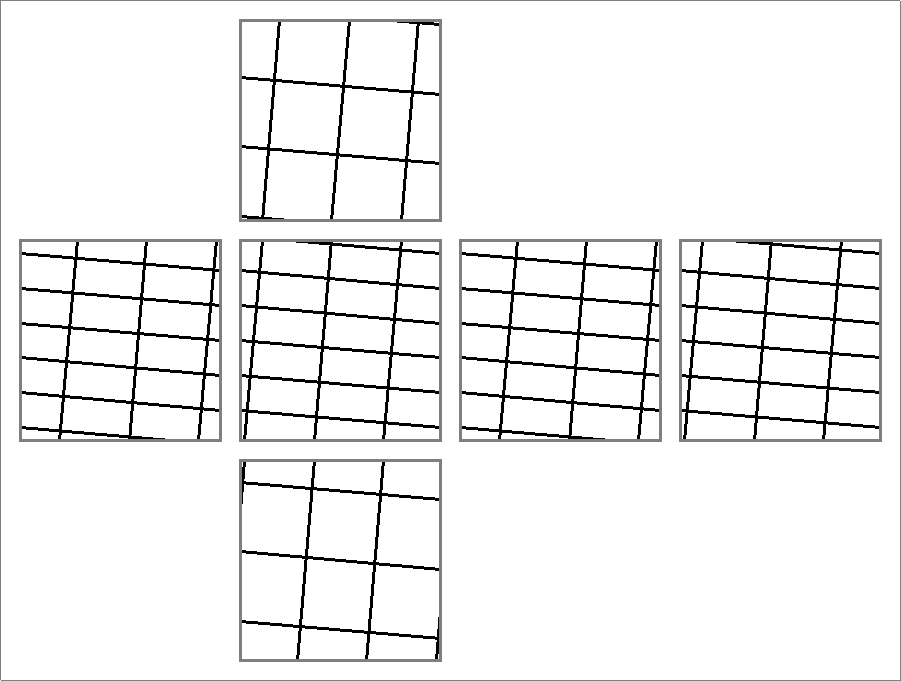
84C			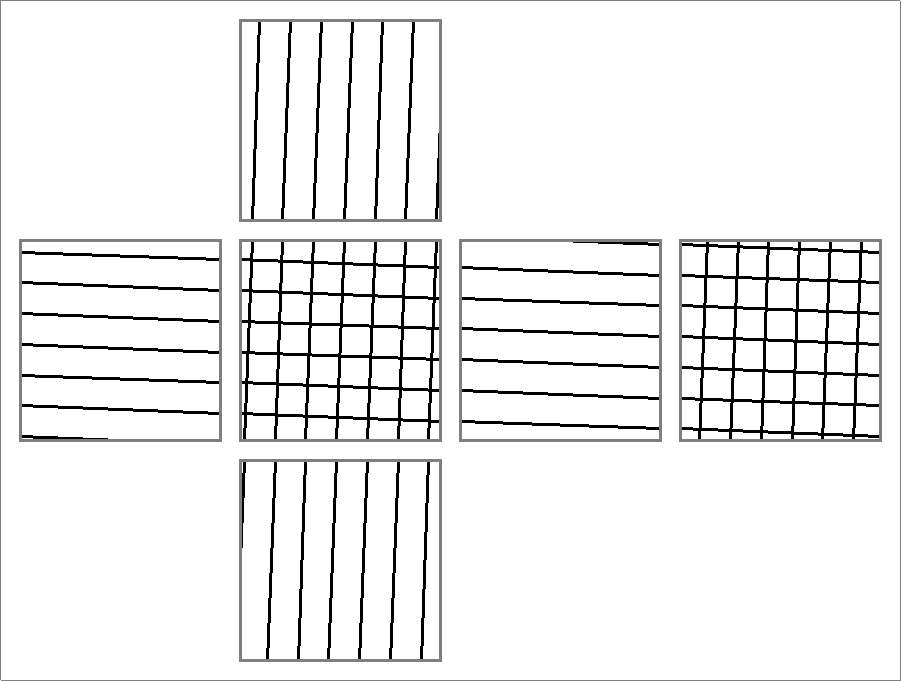	Contains double edges Same as Octahedron-84F and Icosahedron-84B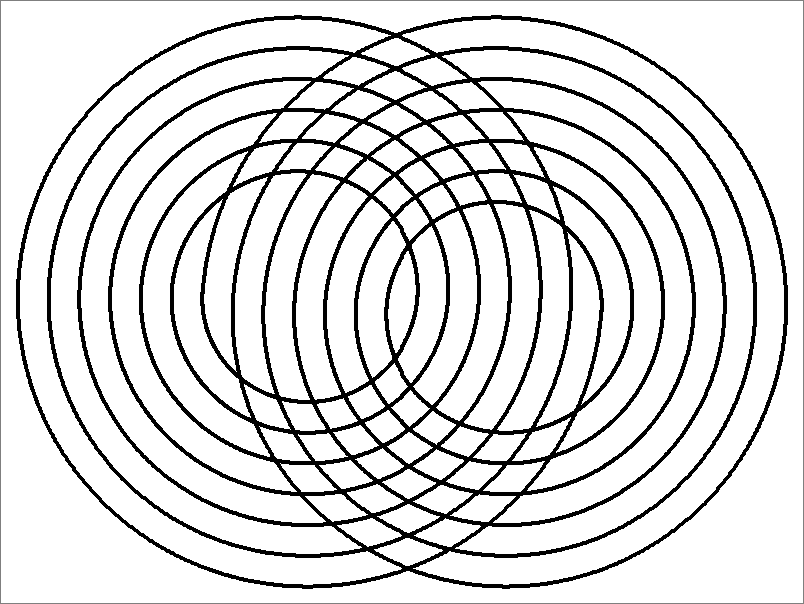
88A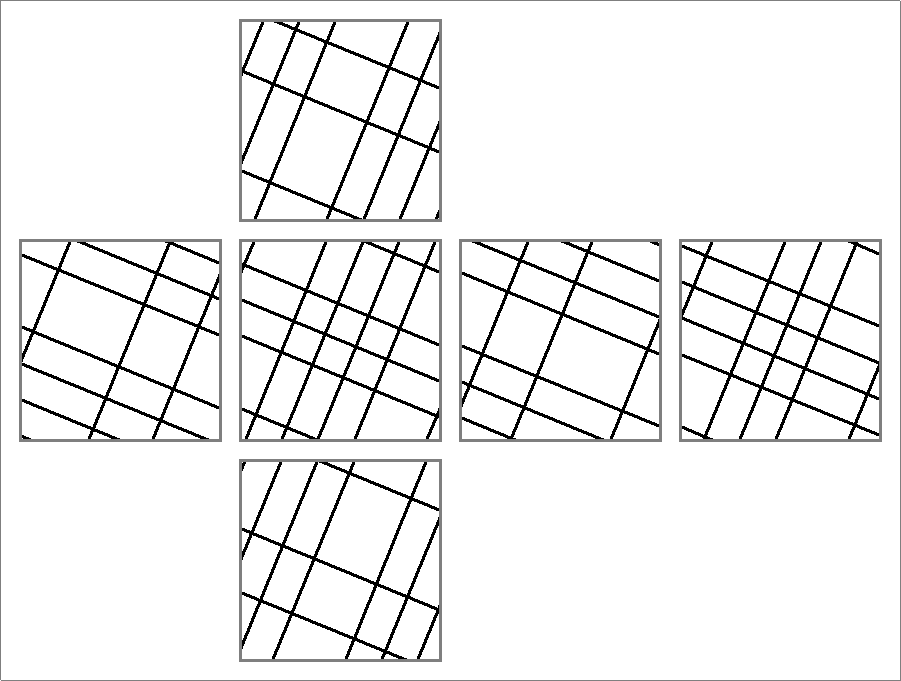
88B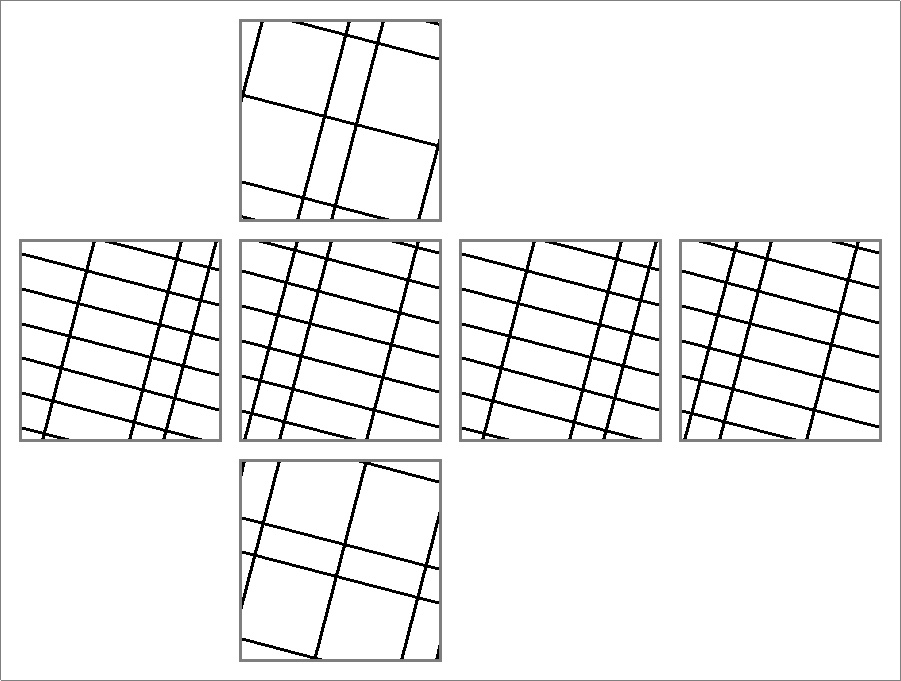
93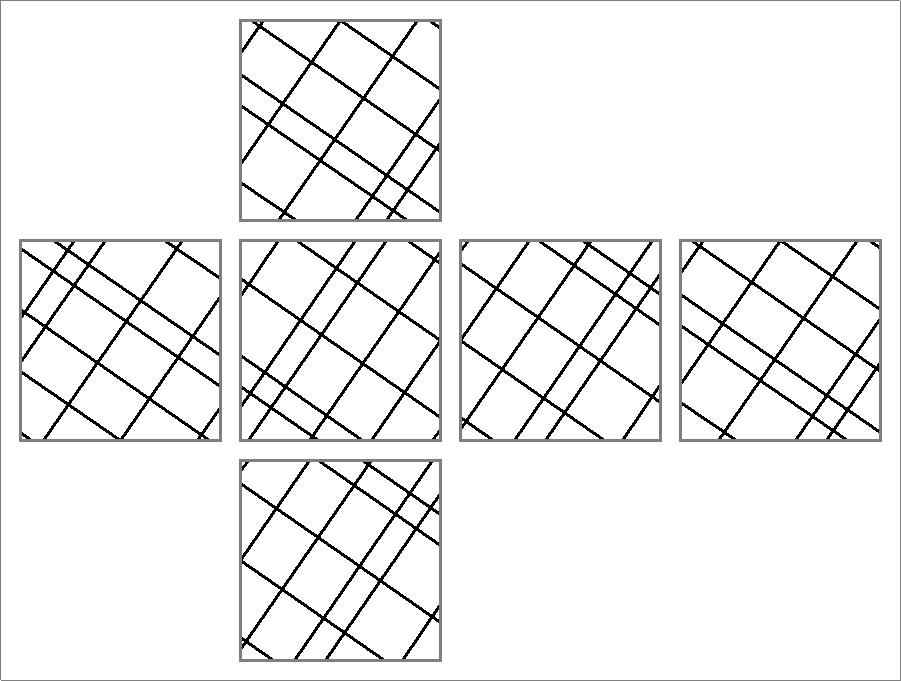
96A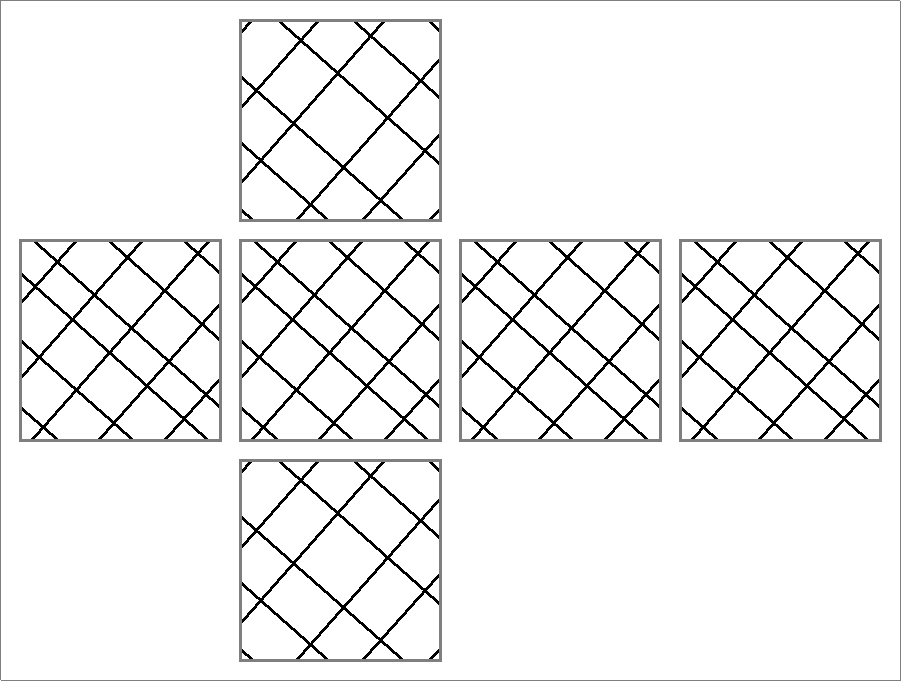
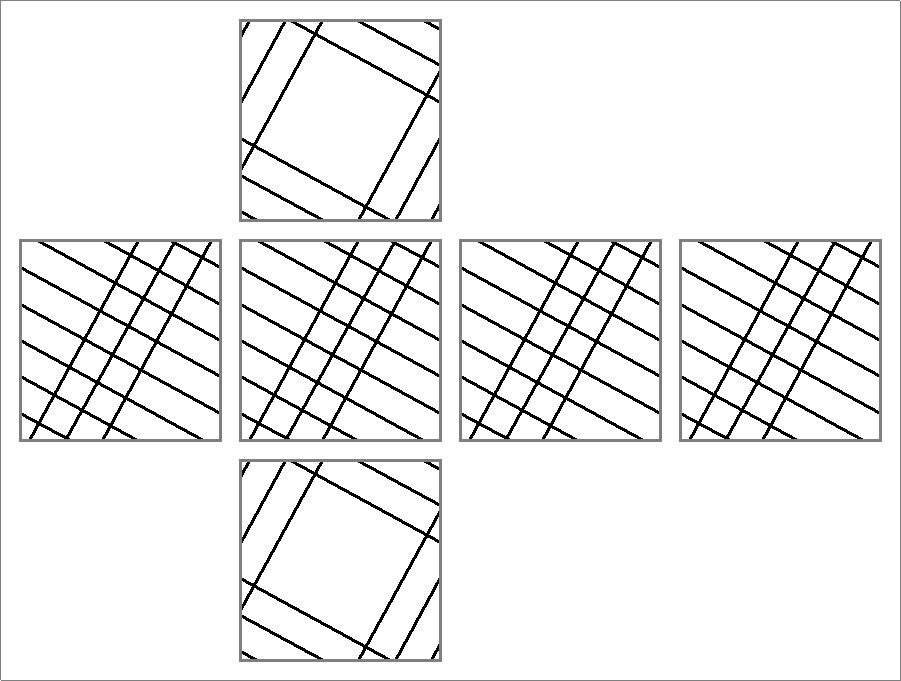96B
96C
96D				Same as Icosahedron-96B
96E
100A
100B
104A
104B
108A				Same as Octahedron-108C and Icosahedron-108A
108B				Same as Icosahedron-108B
108C
108D				Same as Icosahedron-108C
112A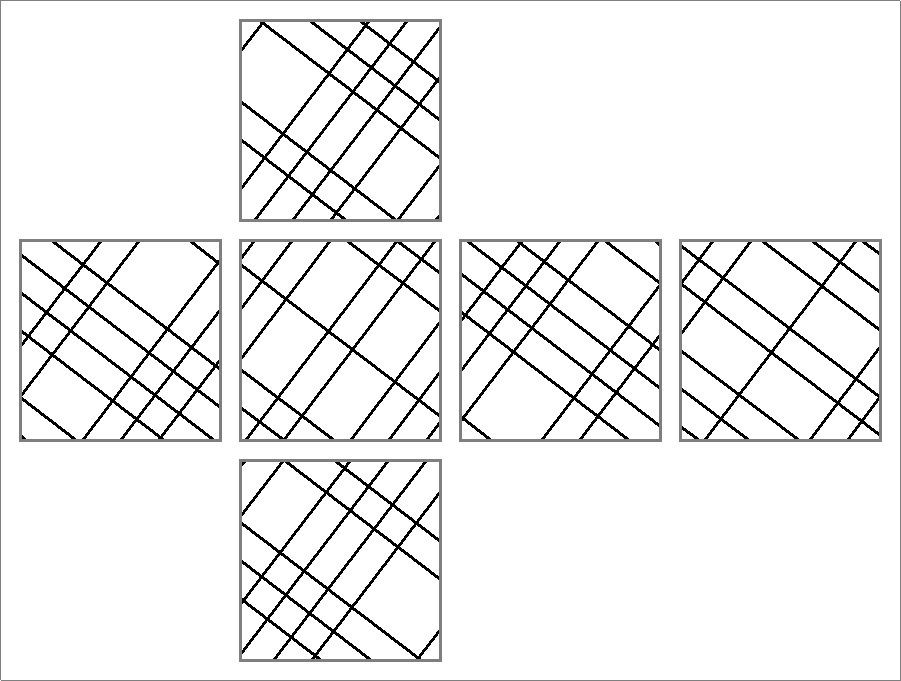
112B			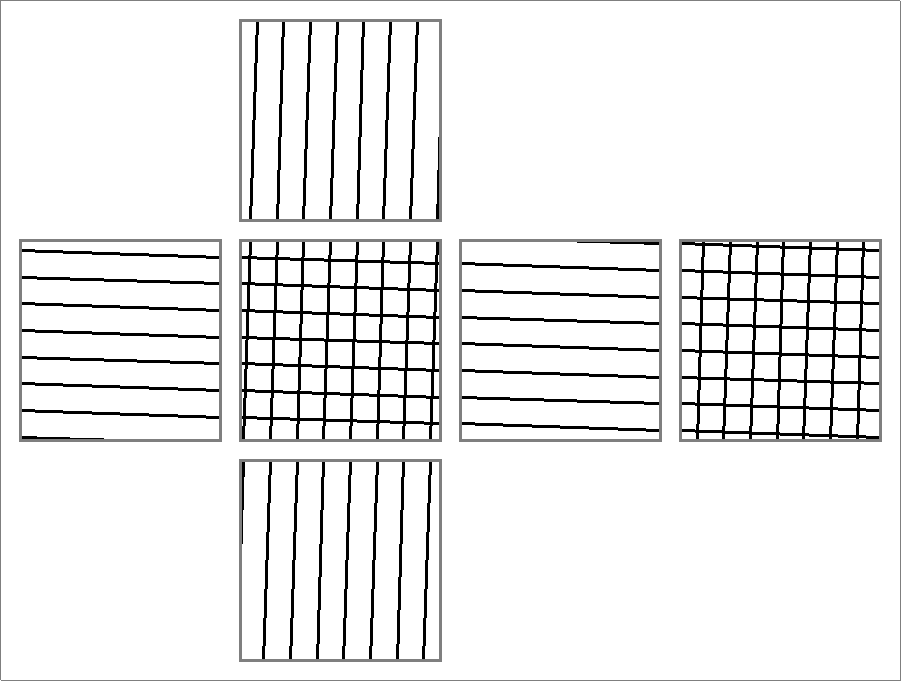	Contains double edges Same as Octahedron-112B and Icosahedron-112B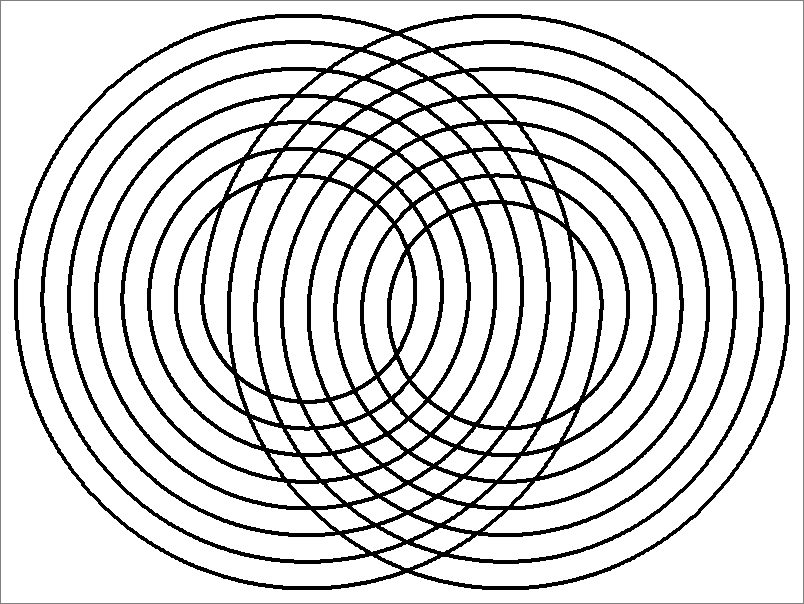
114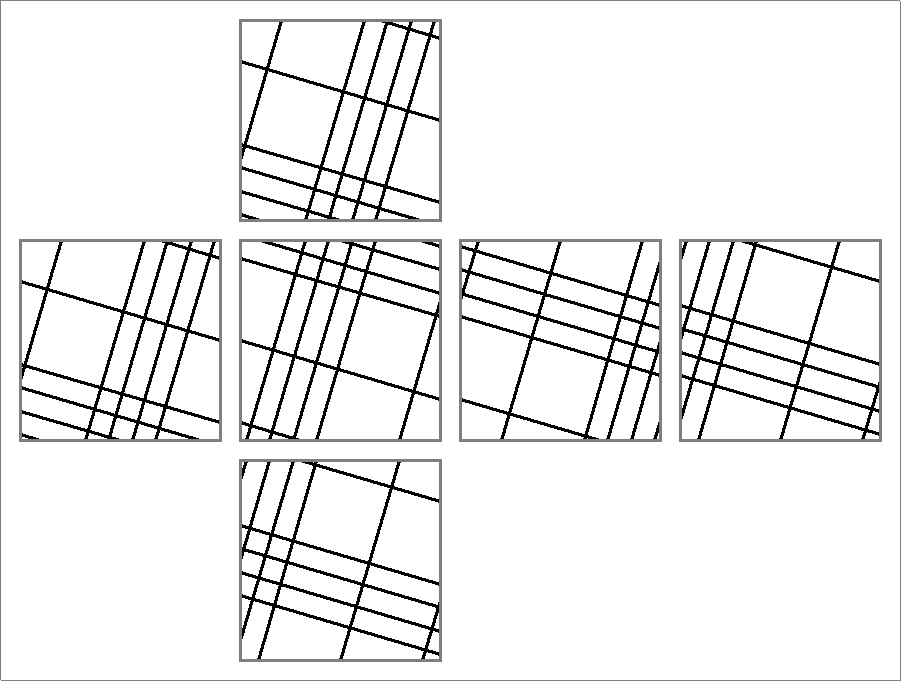
116
120A
120B
120C
120D
126
128A
128B
128C
128D				Same as Icosahedron-128
129
135A				Same as Octahedron-135G and Icosahedron-135B
135B				Same as Icosahedron-135C
135C				Same as Icosahedron-135A
136
144A
144B
144C			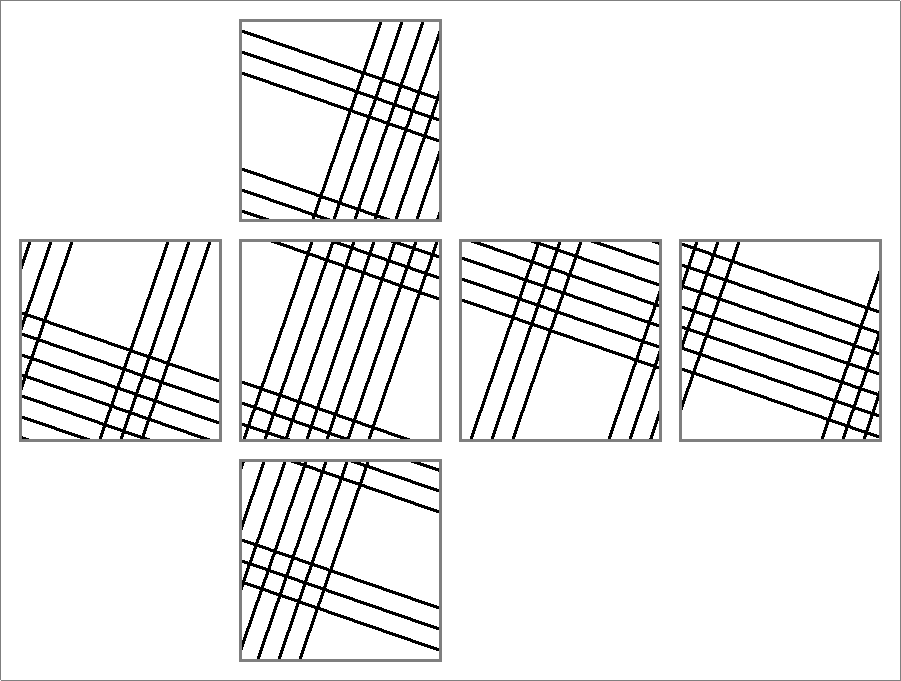	Same as Icosahedron-144B
144D			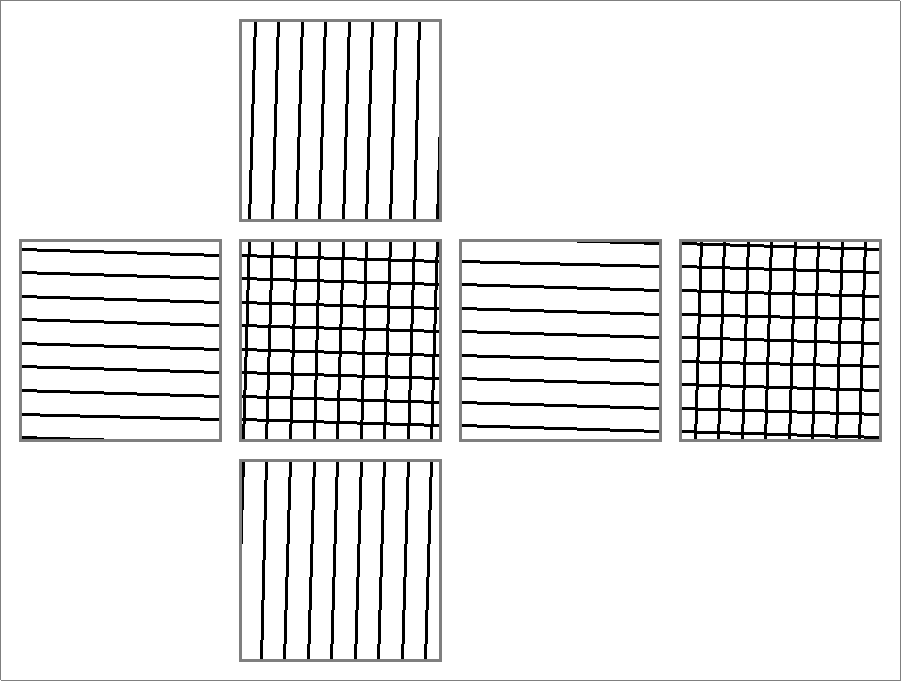	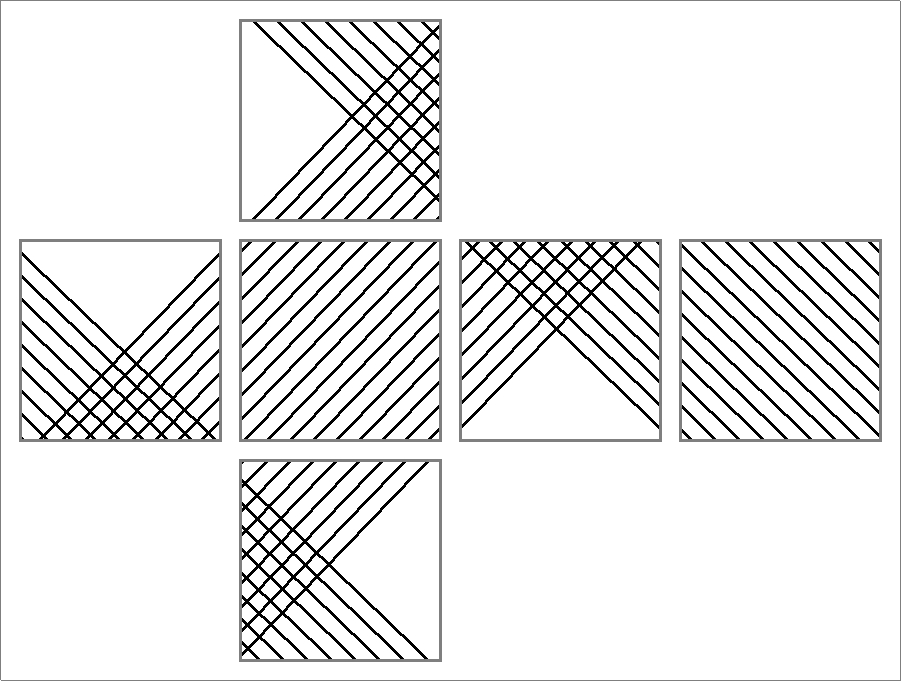Contains double edges Same as Octahedron-144E and Icosahedron-144C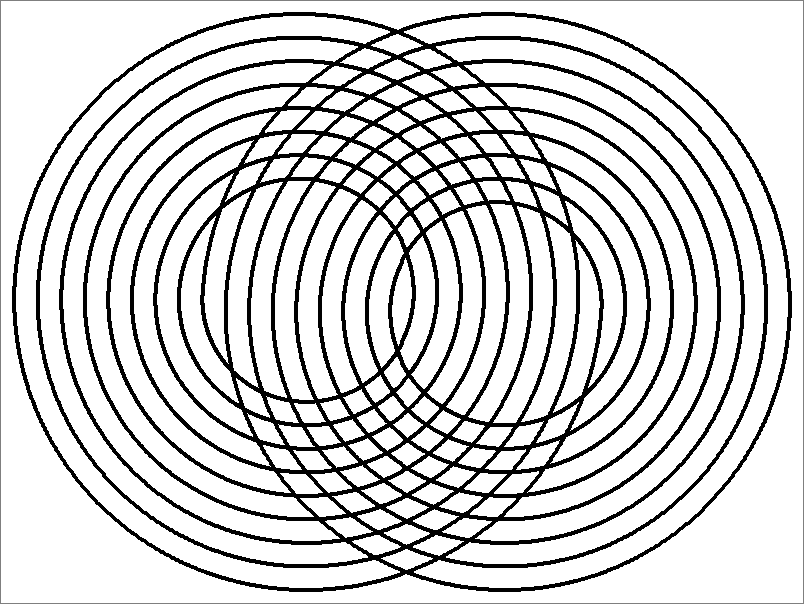
148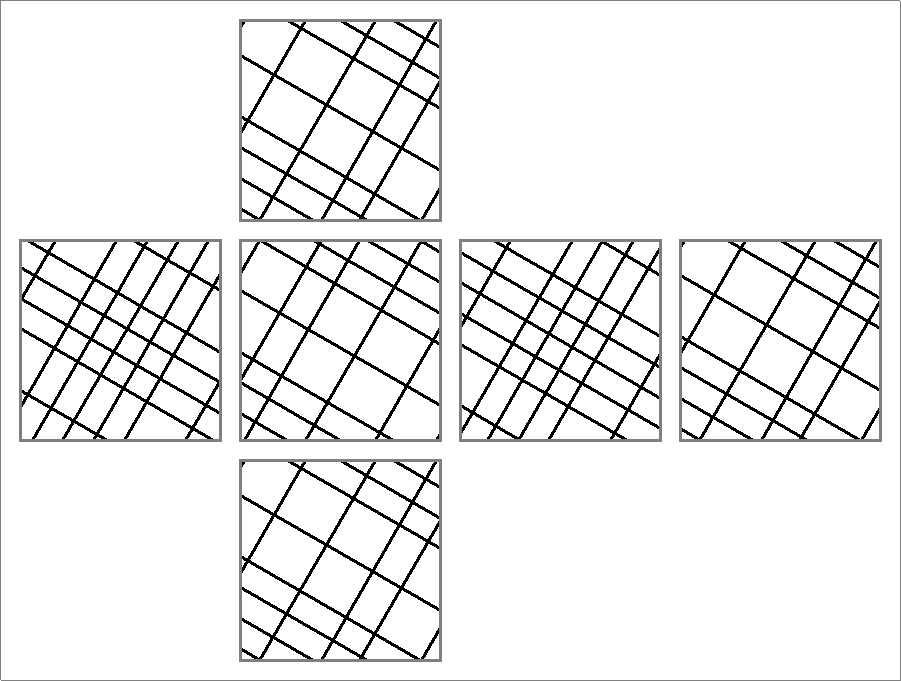
150A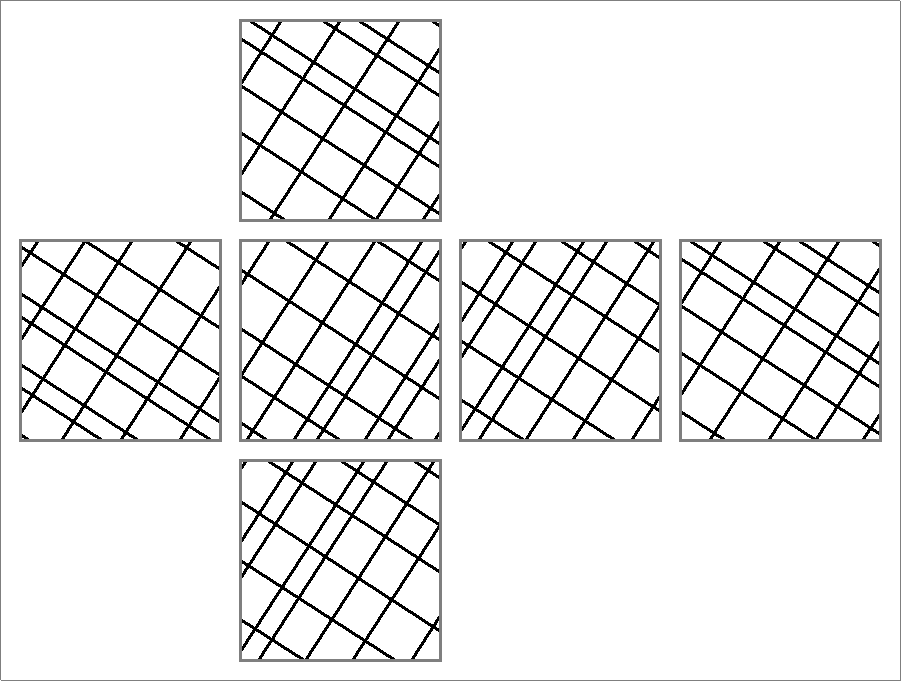
150B
152A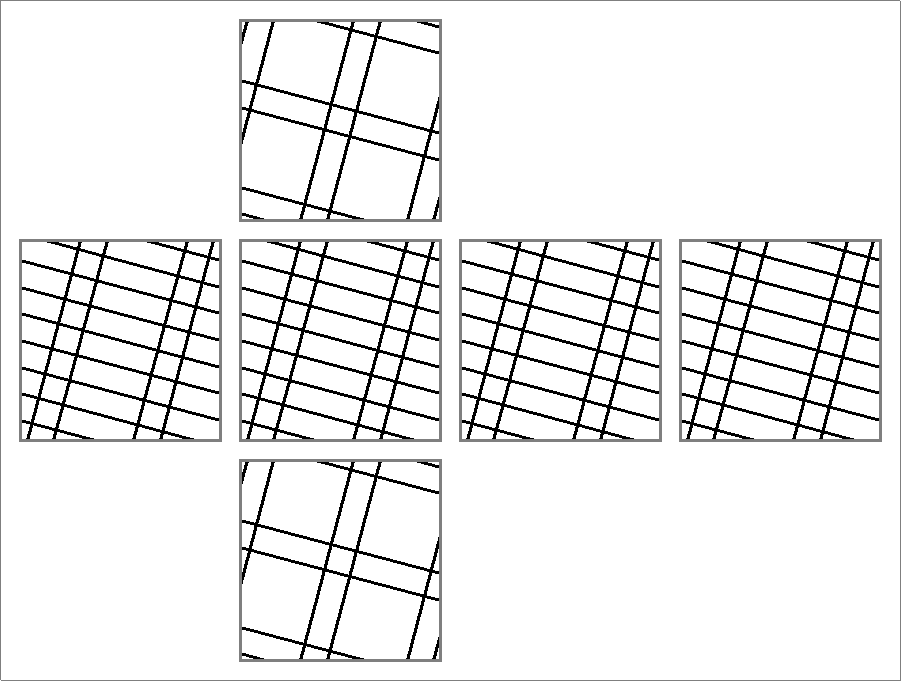
152B
156A
156B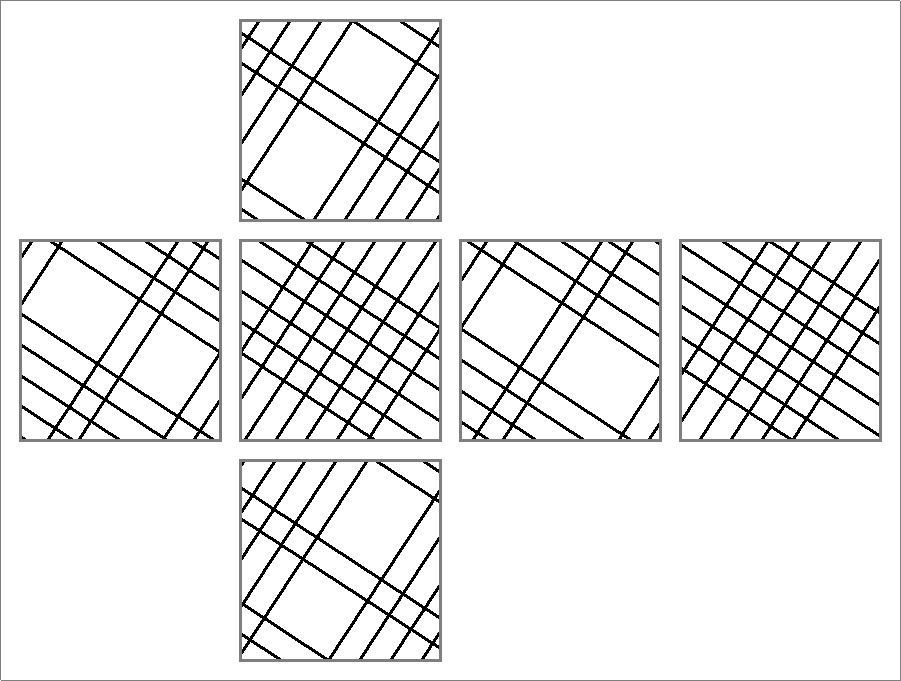
156C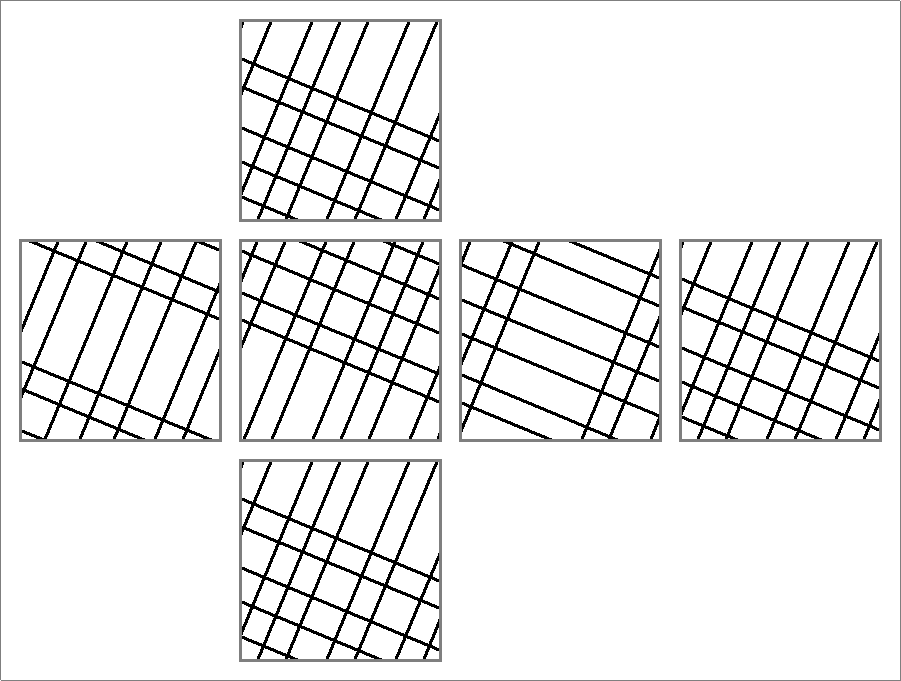
164A			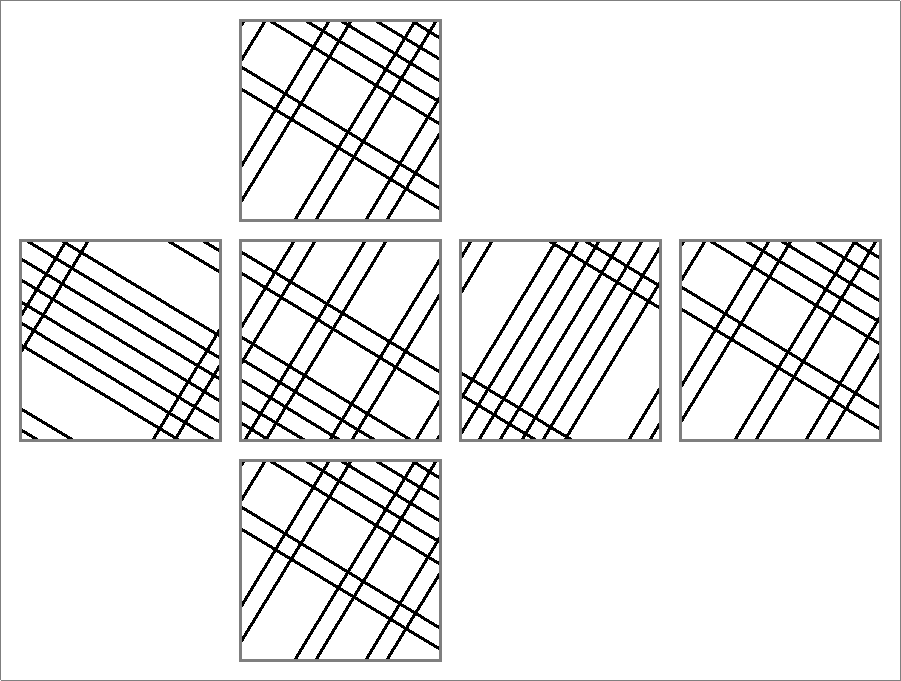	Same as Icosahedron-164A
164B			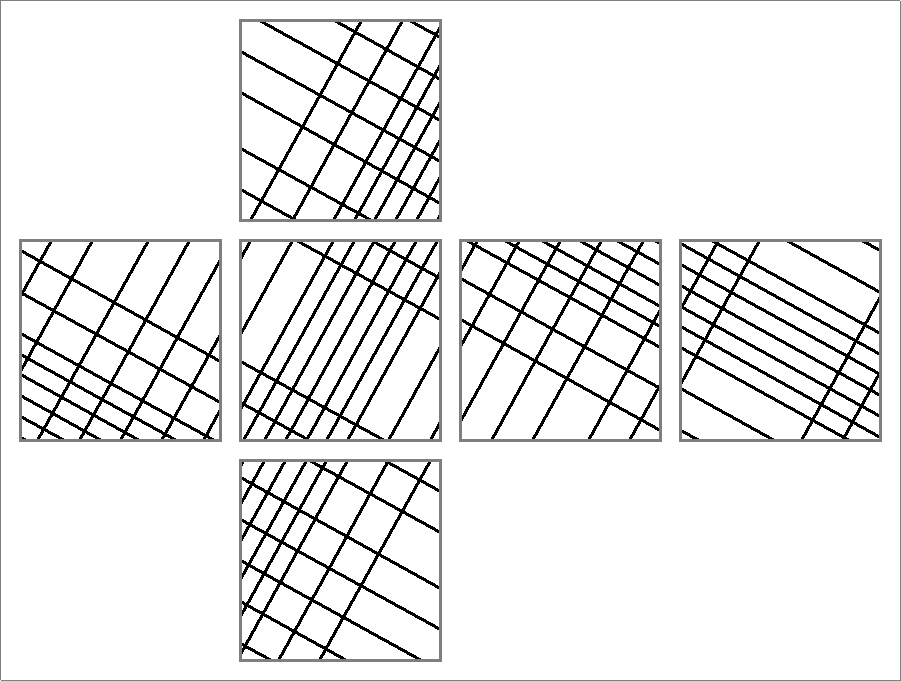	Same as Icosahedron-164B
165A			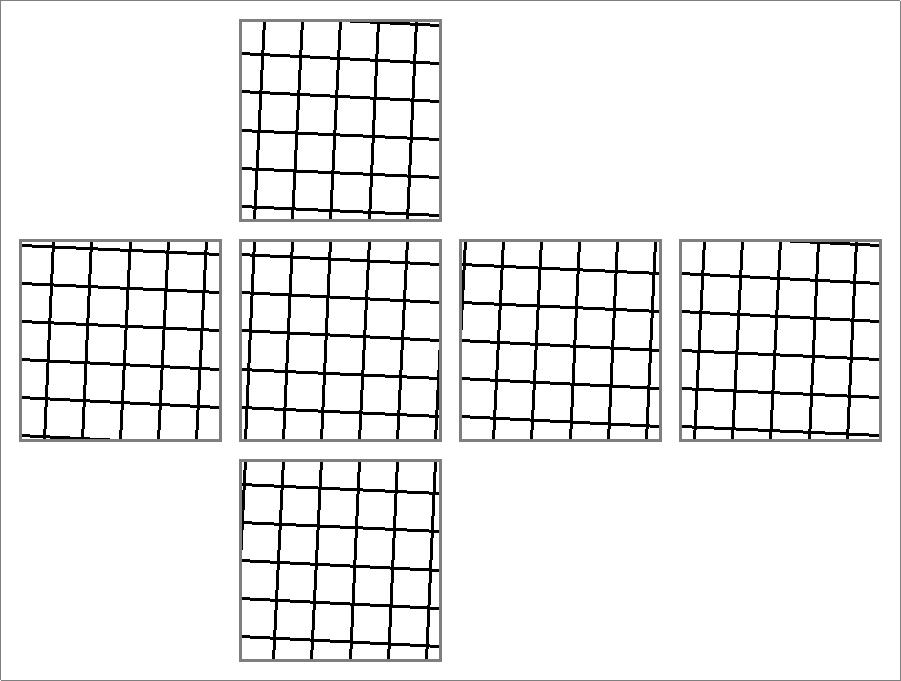	Same as Octahedron-165A and Icosahedron-165D
165B				Same as Icosahedron-165C
168
171A
171B
174
176A
176B
176C
180				Contains double edges Same as Octahedron-180E and Icosahedron-180
184A
184B
184C				Same as Icosahedron-184
192
195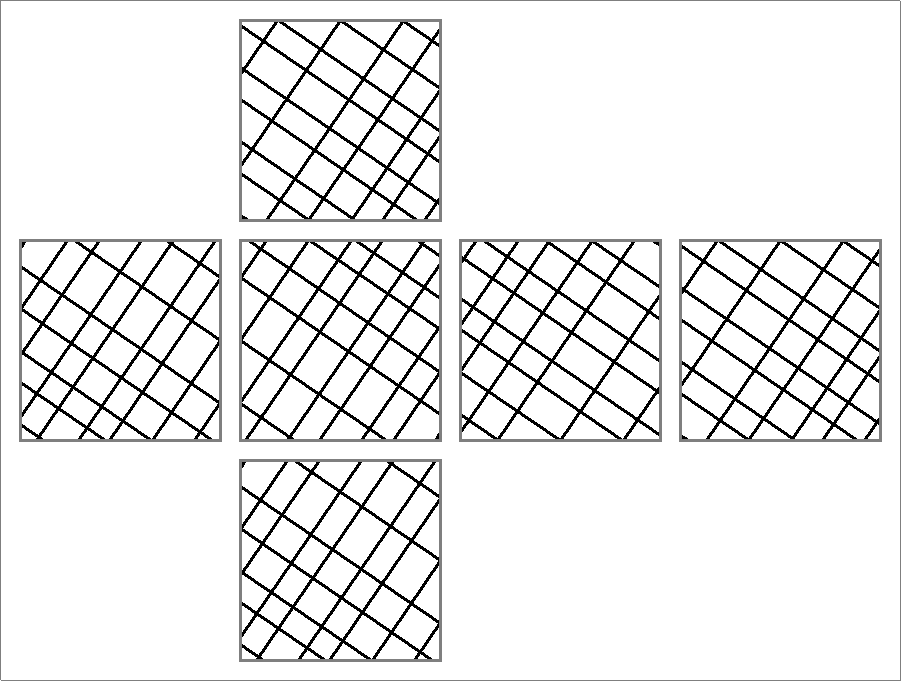
196
198A				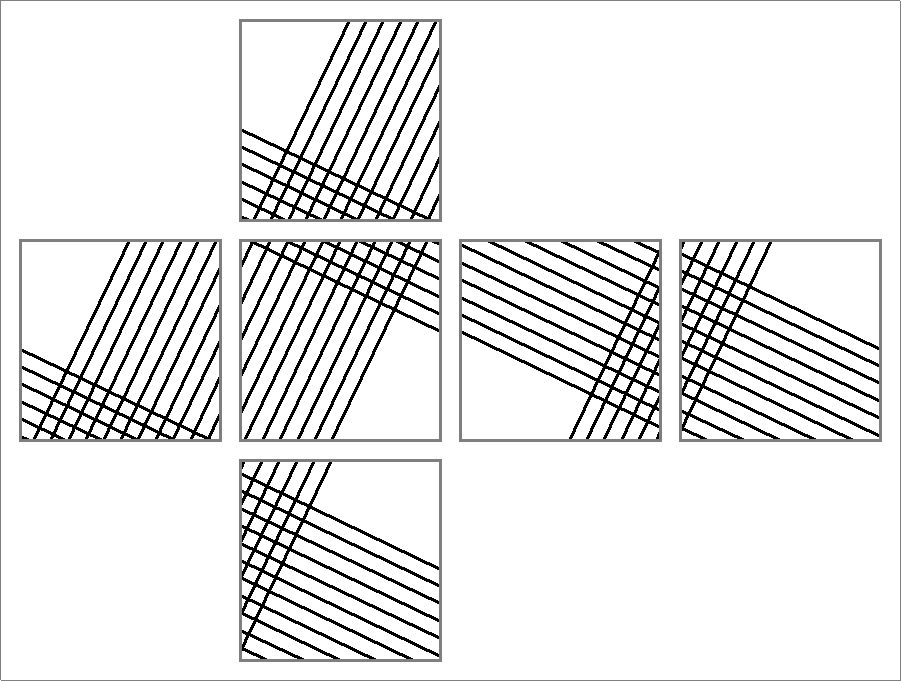Same as Octahedron-198G and Icosahedron-198B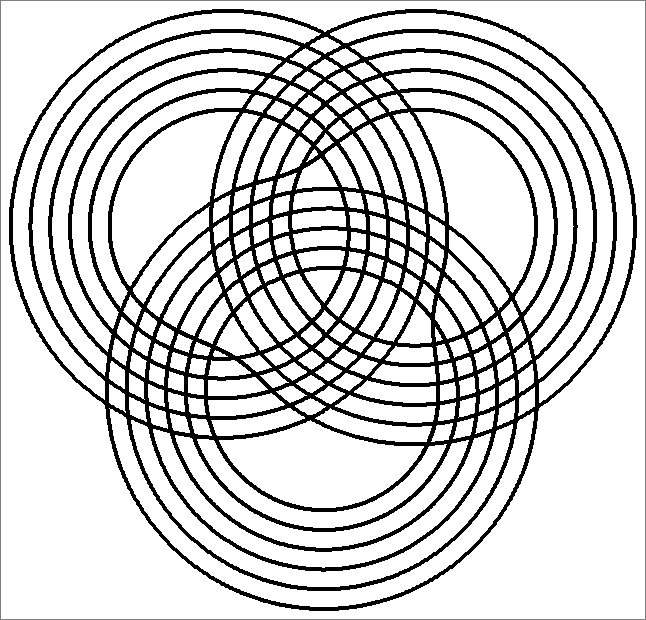
198B			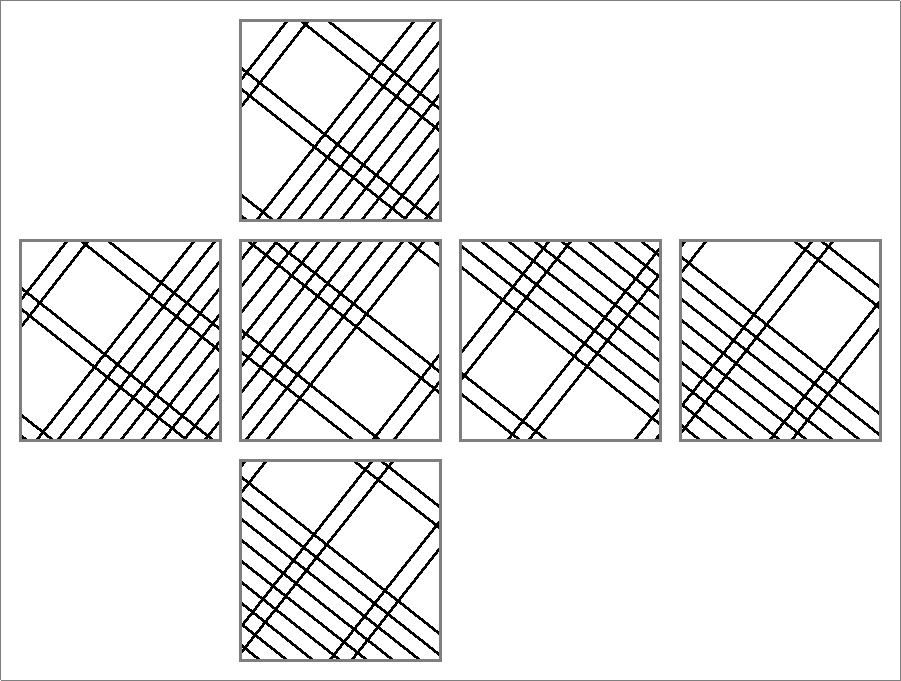	Same as Icosahedron-198A
200A
200B
200C
200D				Same as Icosahedron-200