| Tours | | Illustrations | | Comments | | Additional illustrations |
| 0 | | 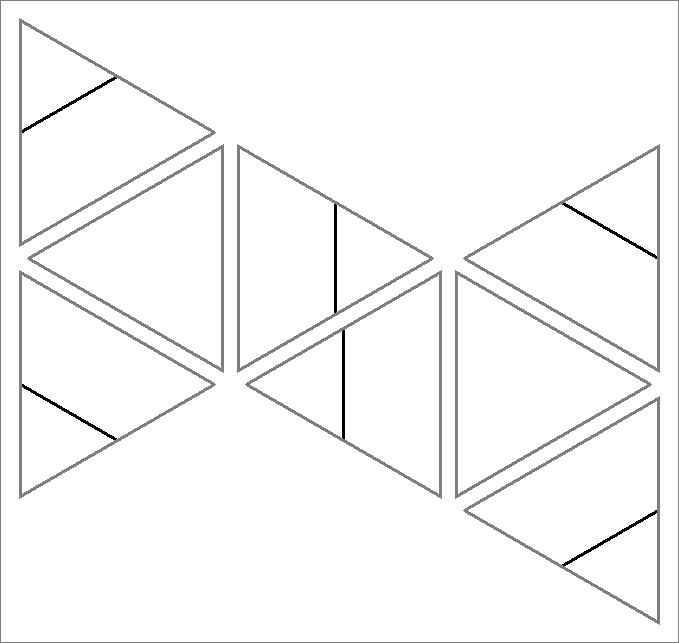
 | | No crossing points
Same as Cube-0
and Icosahedron-0 | | |
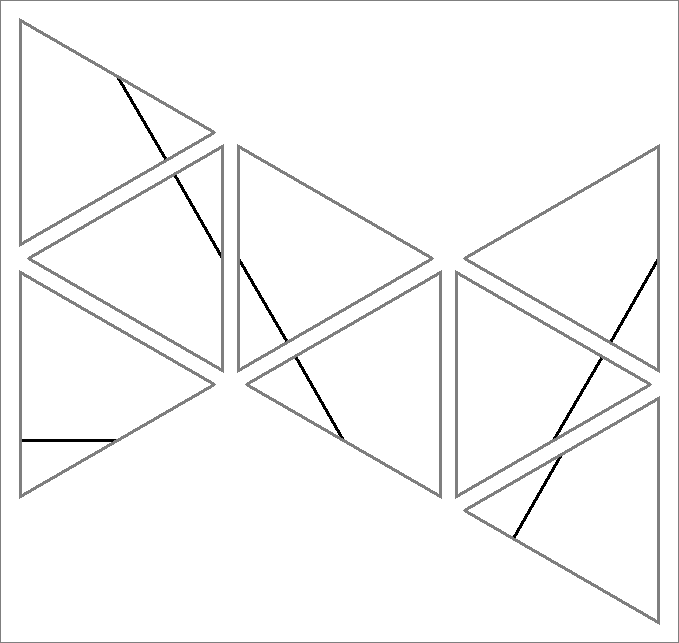
| 3 | | 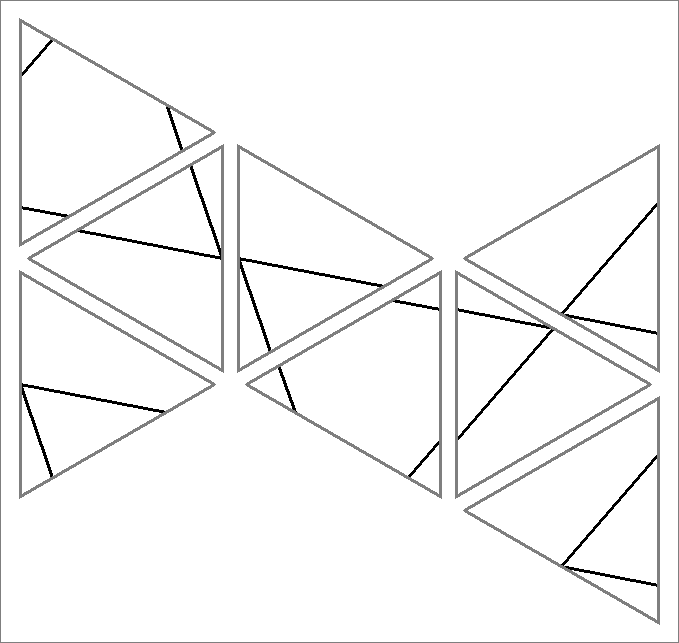 | | Contains
double edges
Same as Cube-3
and Icosahedron-3 | |  |
| 4 | | 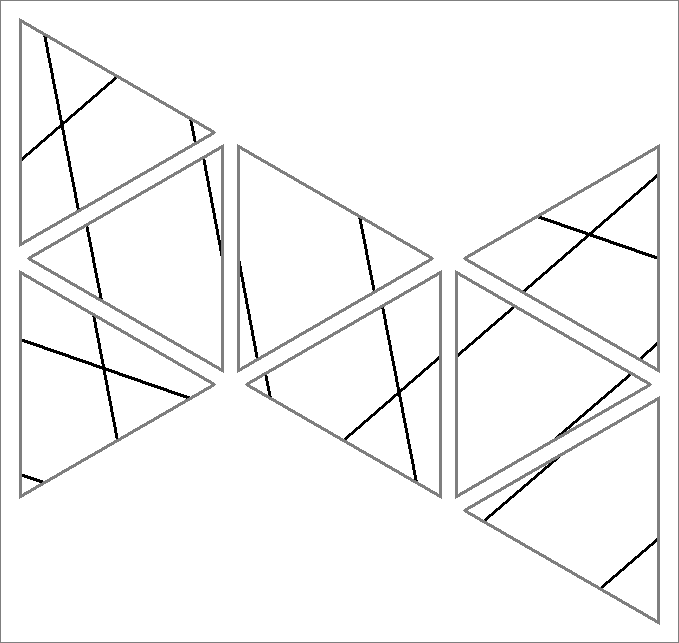 | | Contains
double edges
Same as Cube-4
and Icosahedron-4 | | 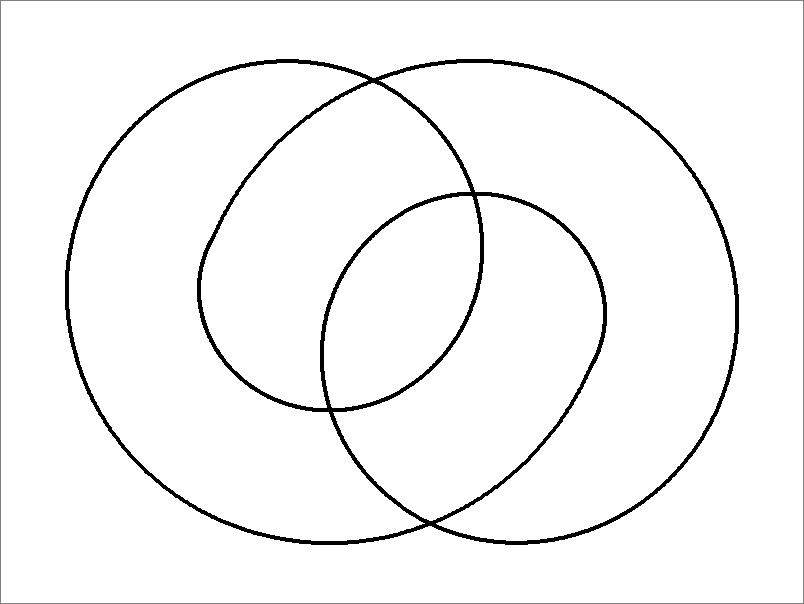 |
| 7x | | 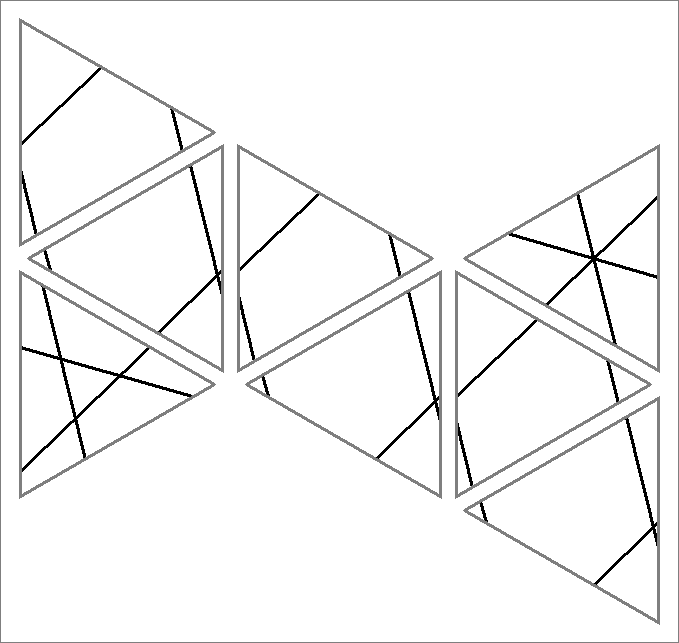 | | Contains
double edges | | 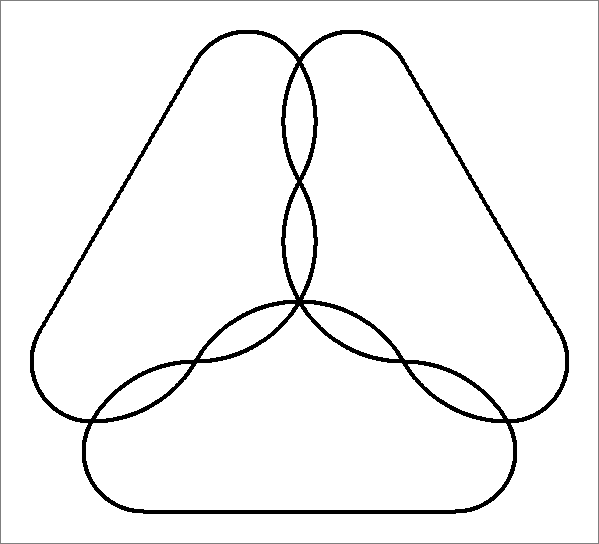 |
| 9A | | 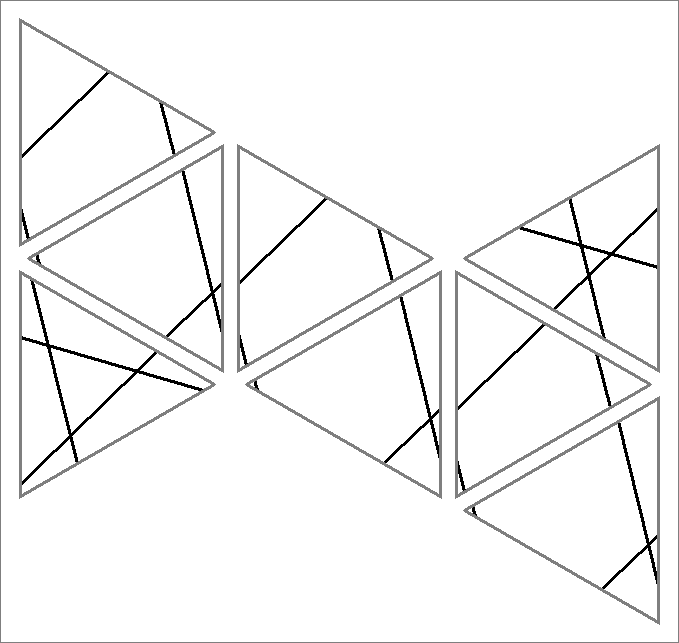 | | Contains
double edges | |  |
| 9B | | 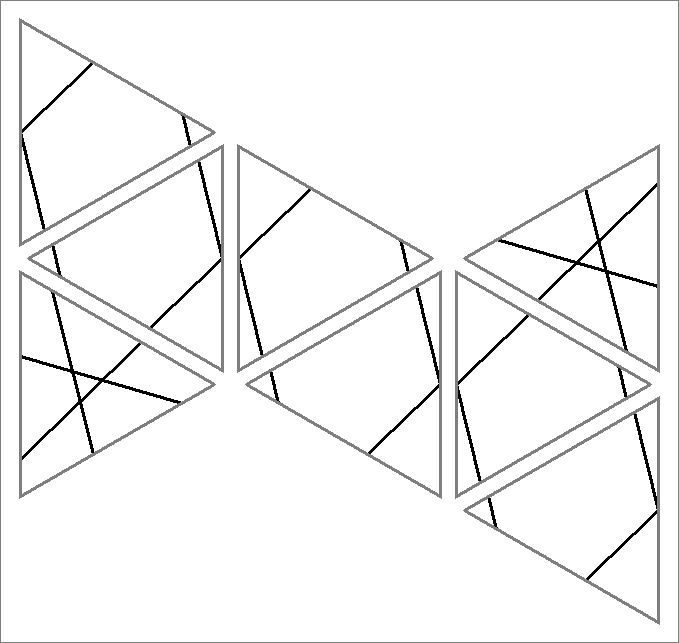 | | Contains
double edges | | 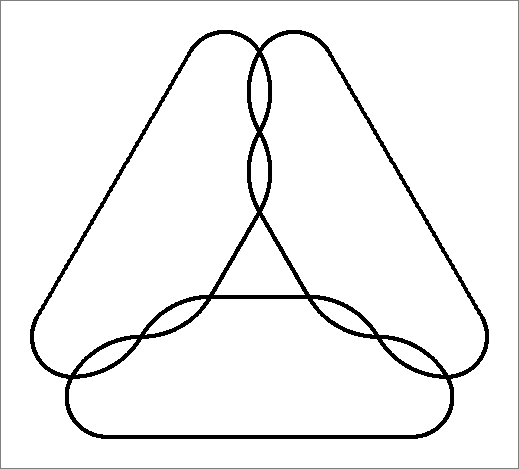 |
| 9C | | 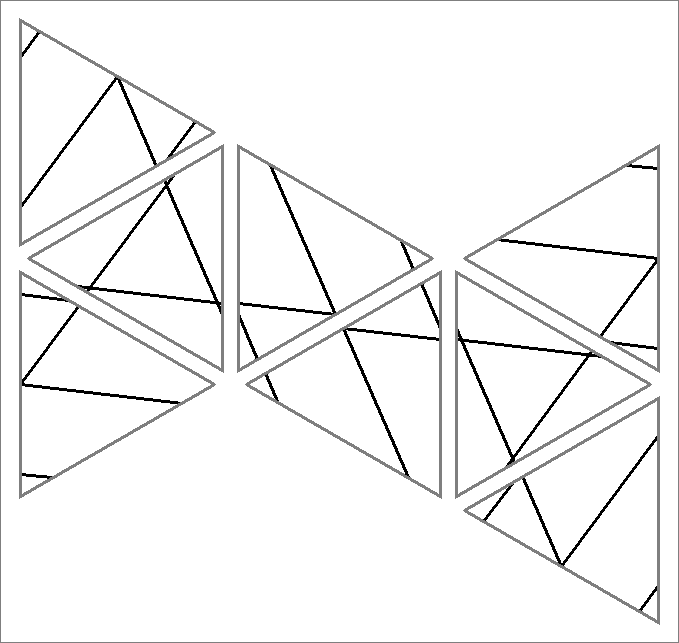 | | Same as Cube-9
and Icosahedron-9 | | 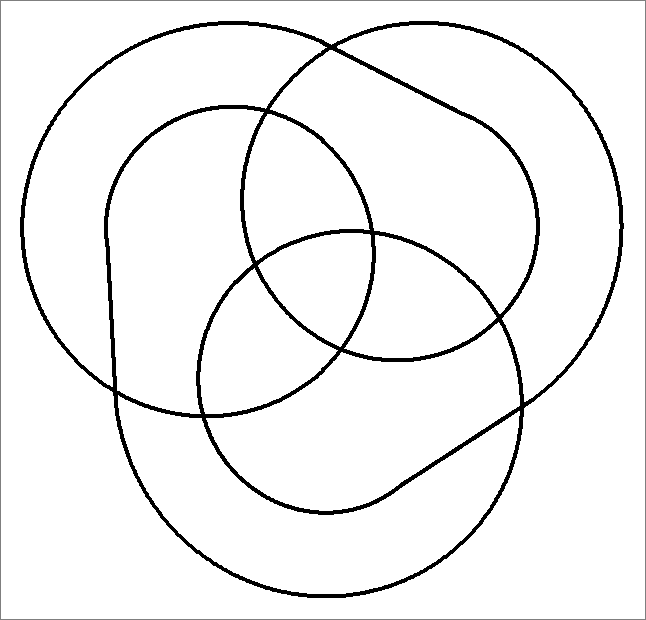 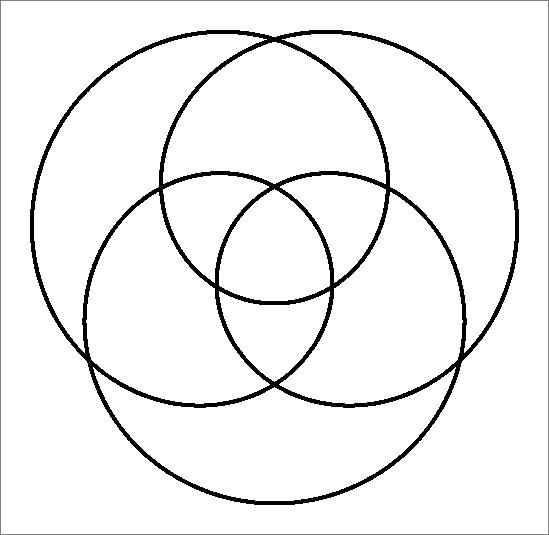 |
| 12A | |  | | Contains
double edges | | 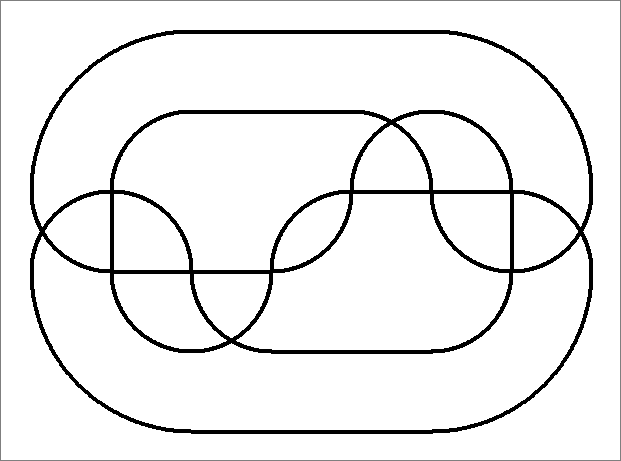 |
| 12B | |  | | Contains
double edges
Same as Cube-12B
and Icosahedron-12 | | 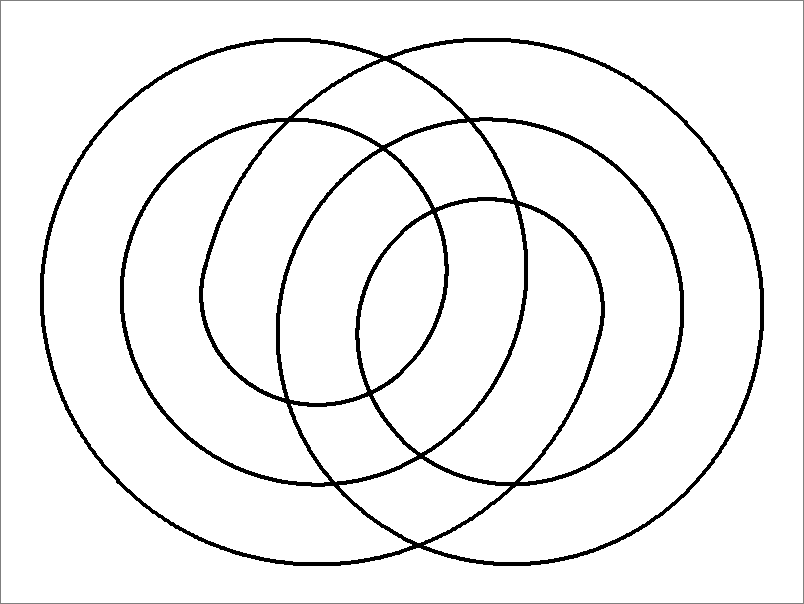 |
| 16x | | 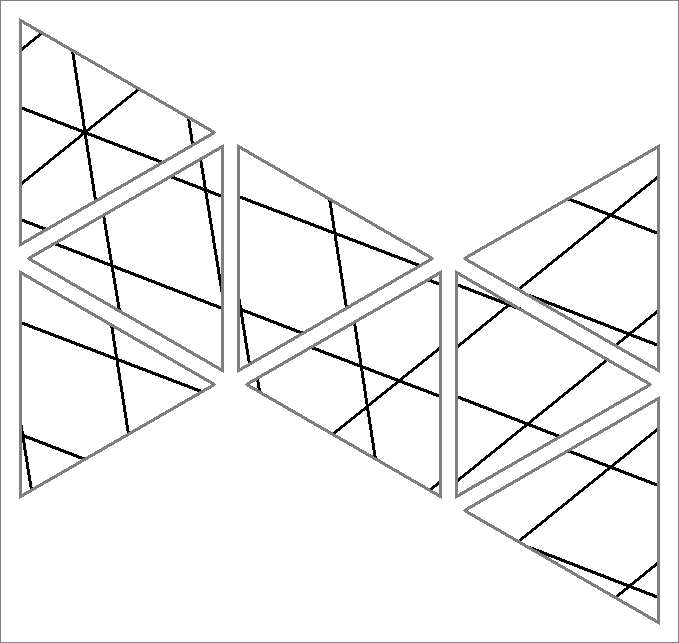 | | | | |
| 18A | | 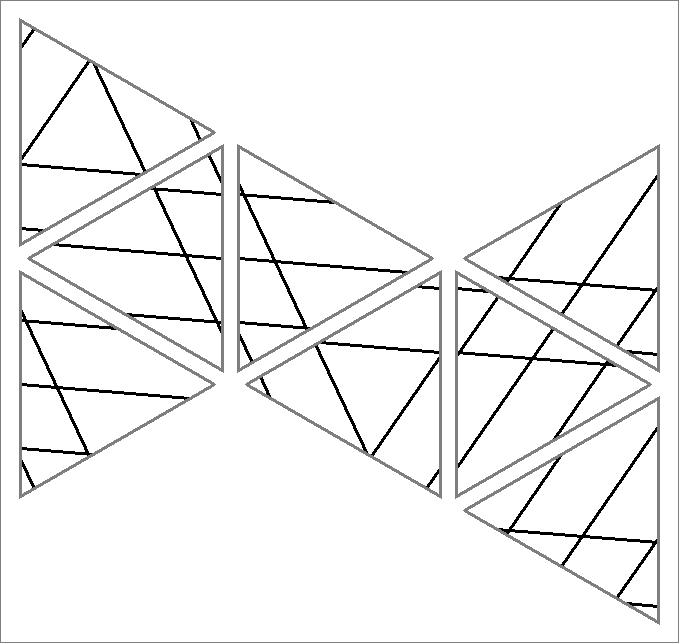
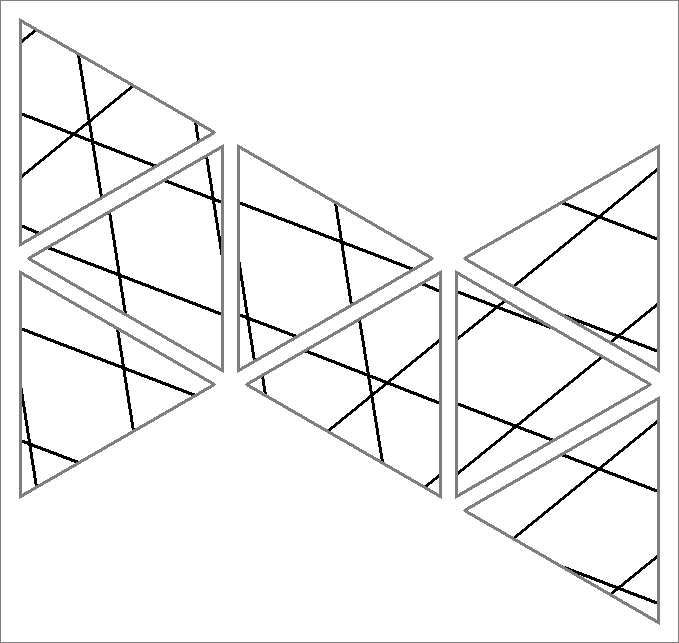 | | Same as Cube-18
and
Icosahedron-18 | |  |
| 18B | | 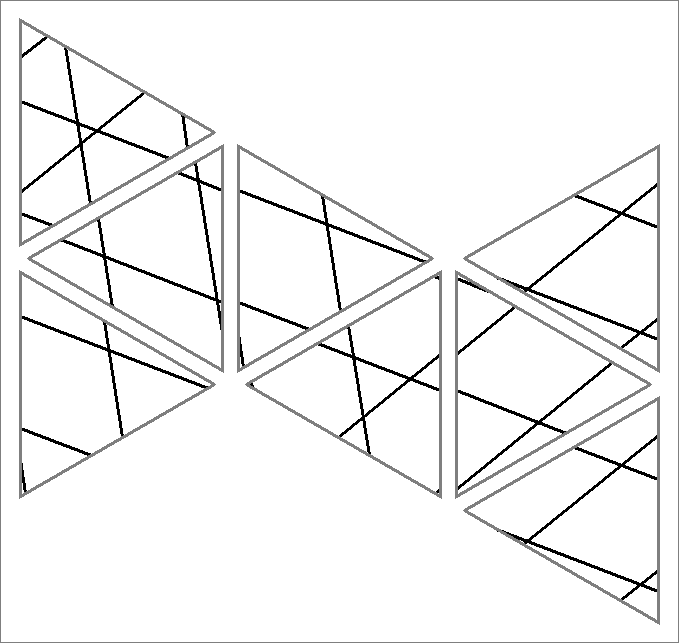 | | | | |
| 24A | | 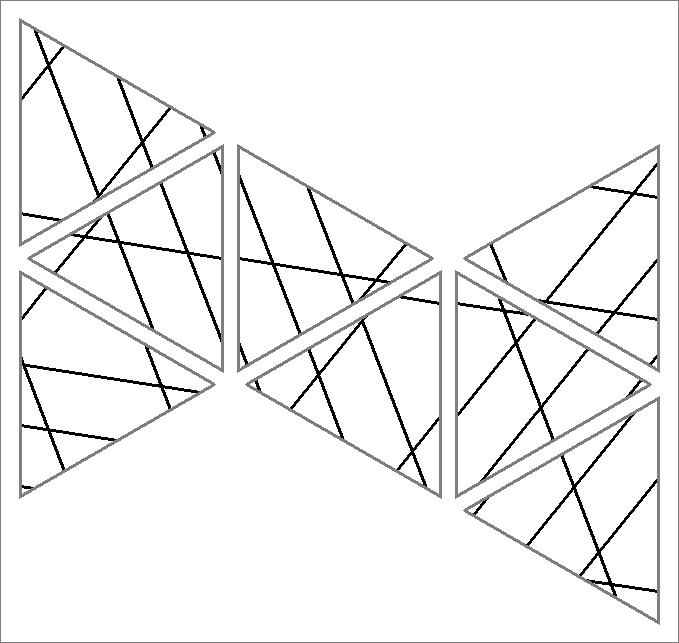 | | Contains
double edges | | |
| 24B | |  | | Contains
double edges
Same as Cube-24C
and Icosahedron-24C | | 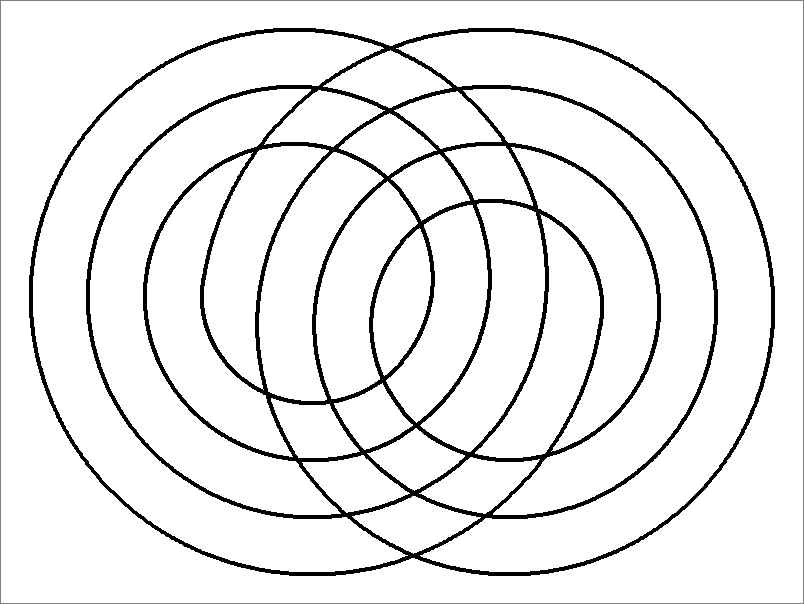 |
| 24x | | 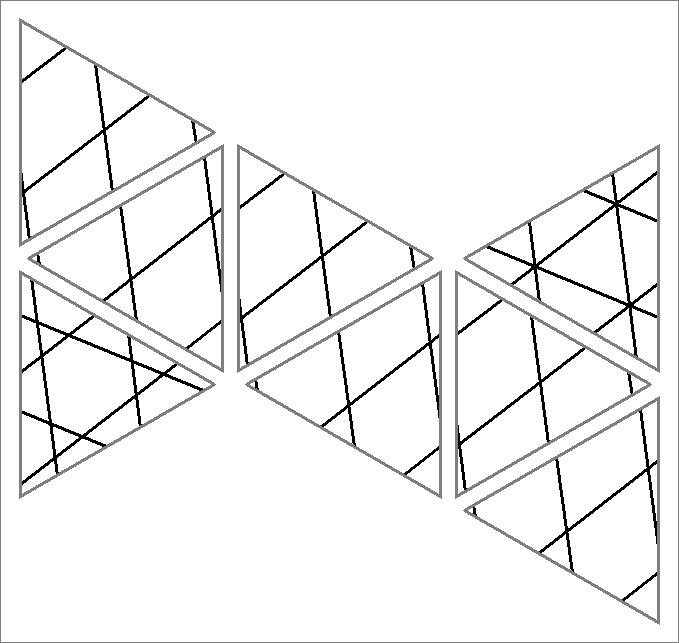 | | Contains
double edges | | |
| 30A | | 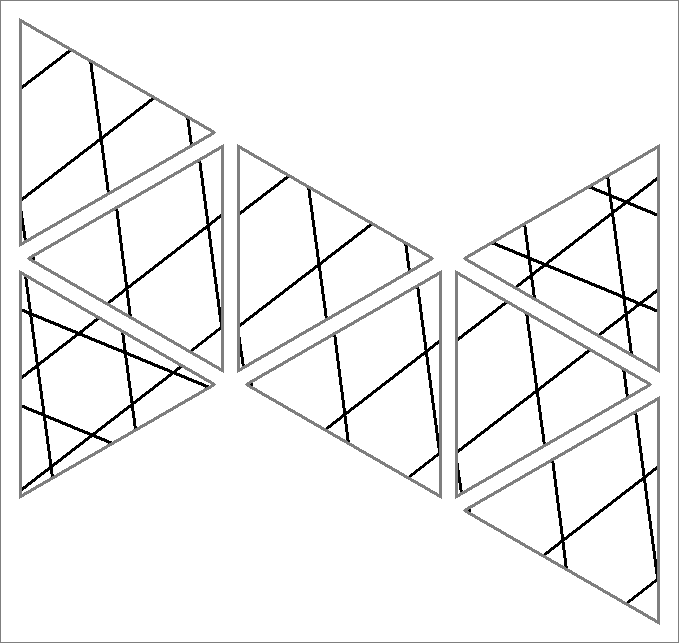 | | Contains
double edges | | |
| 30B | | 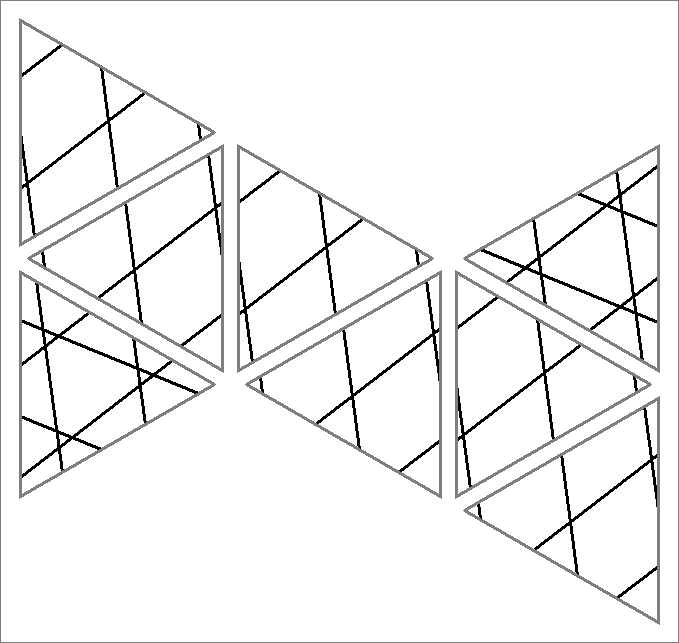 | | Contains
double edges | | |
| 30C | | 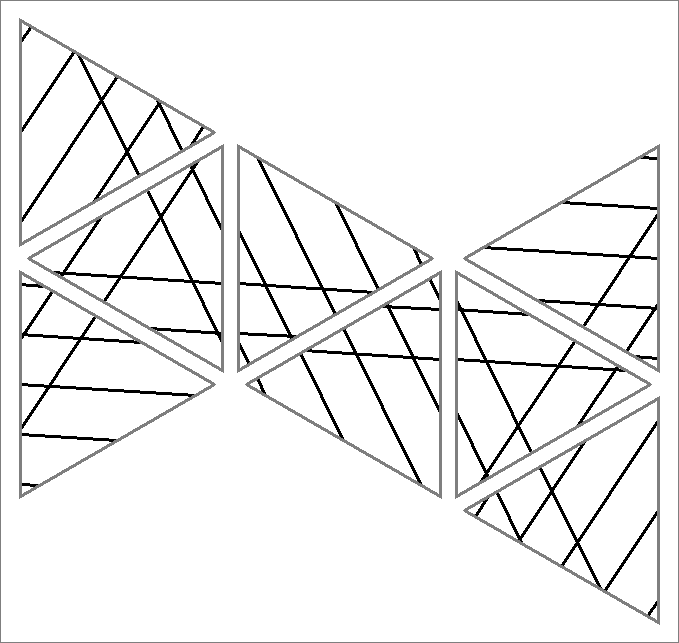 | | Same as Cube-30
and Icosahedron-30 | | 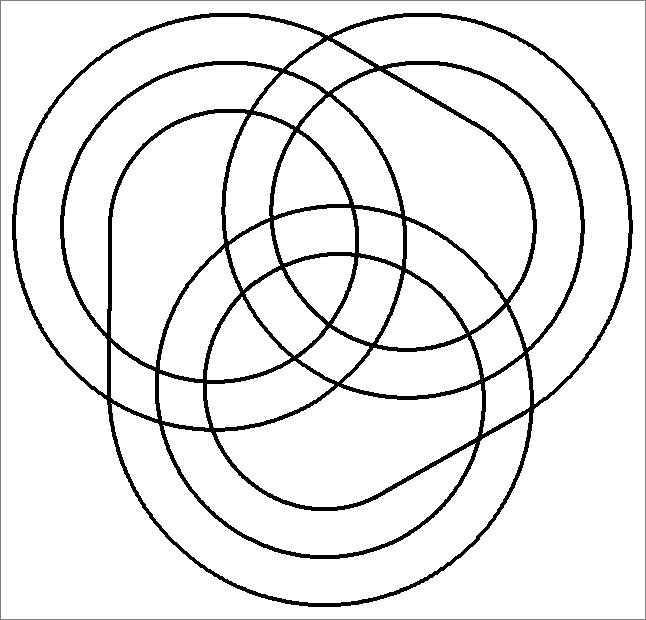 |
| 30x | | 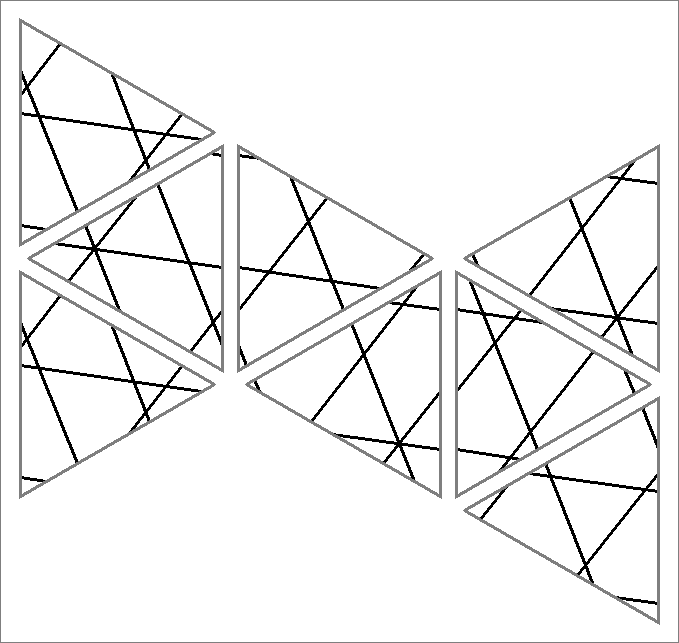 | | Contains
double edges | | |
| 36A | | 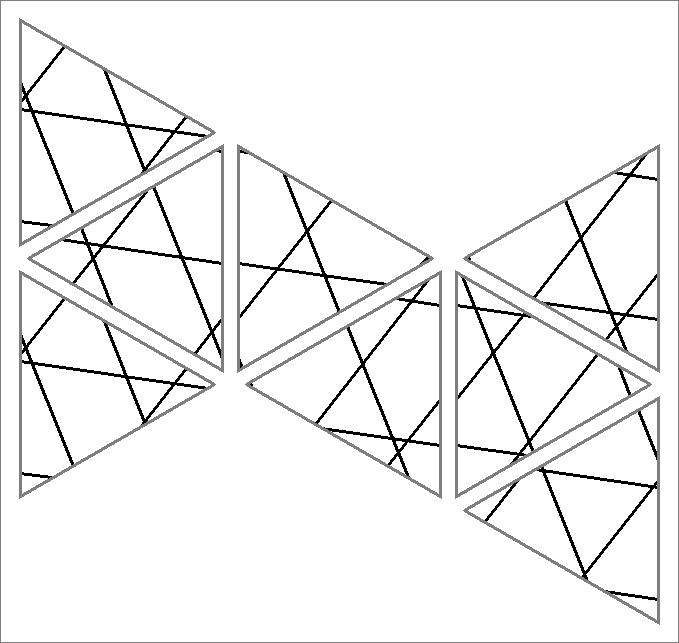 | | Contains
double edges | | |
| 36B | | 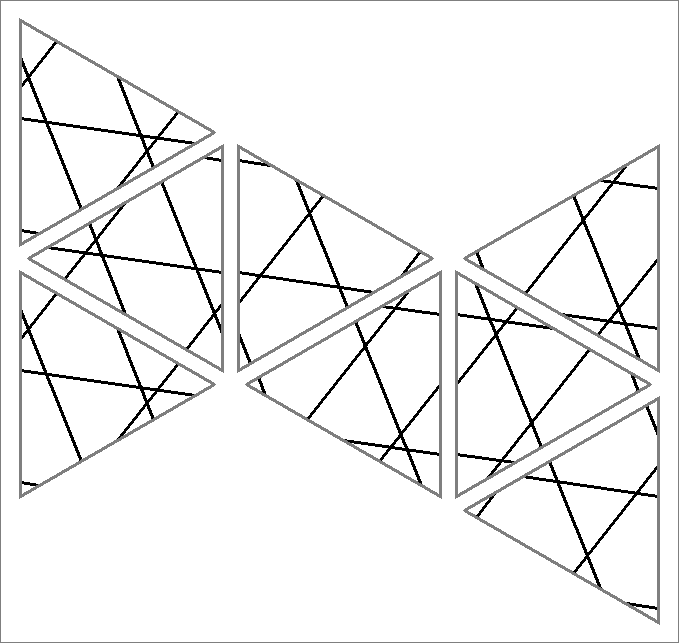 | | Contains
double edges | | |
| 39xA | | 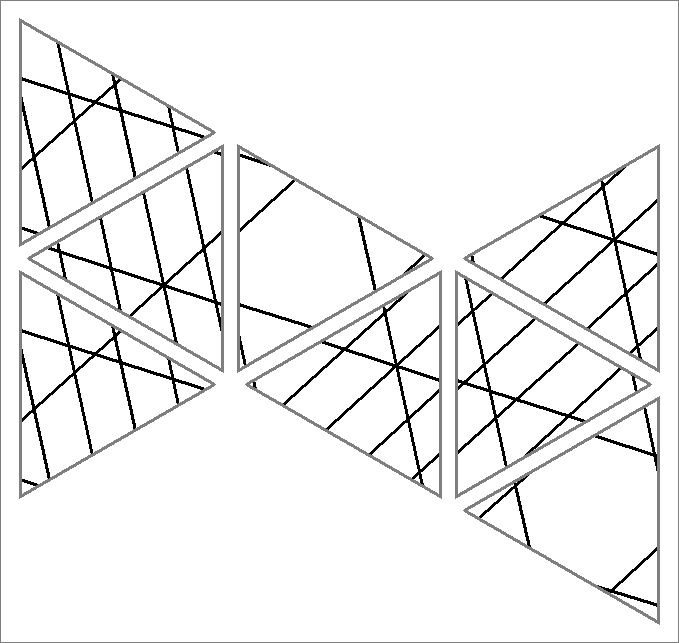 | | | | |
| 39xB | |  | | | | |
| 40A | | 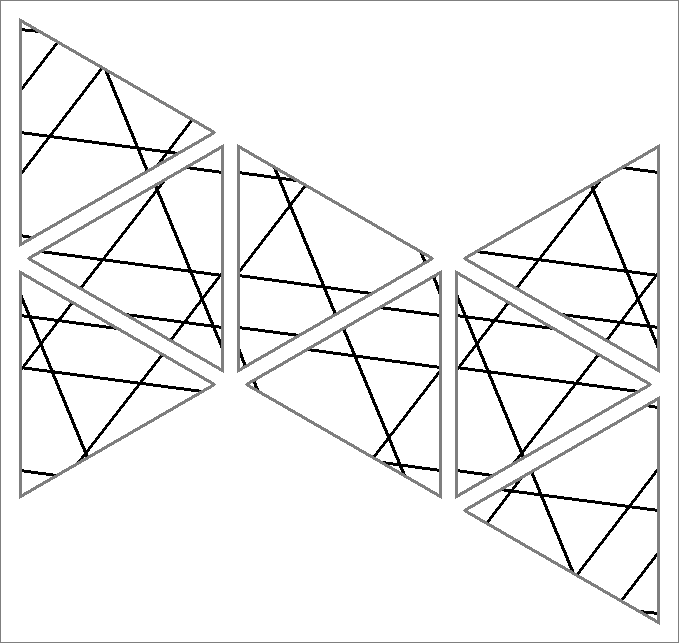 | | Contains
double edges | | |
| 40B | |  | | Contains
double edges
Same as Cube-40B
and Icosahedron-40B | | 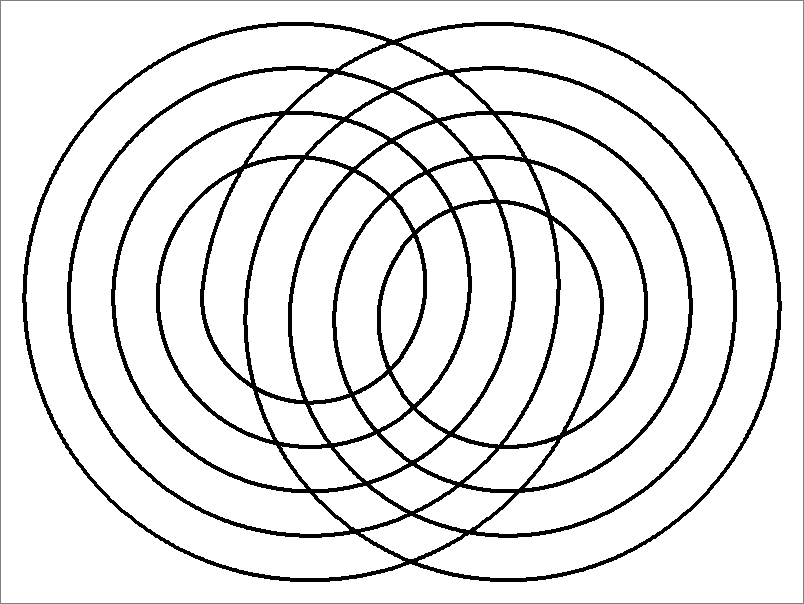 |
| 45A | |  | | | | |
| 45B | | 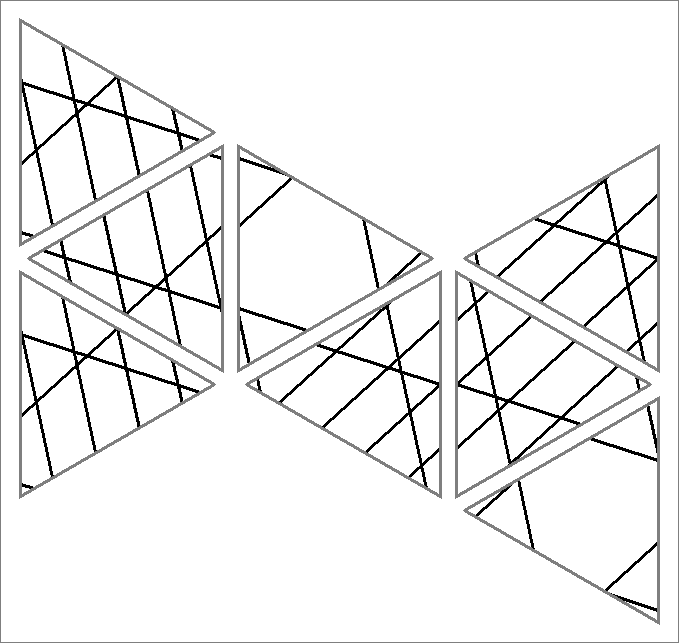 | | | | |
| 45C | | 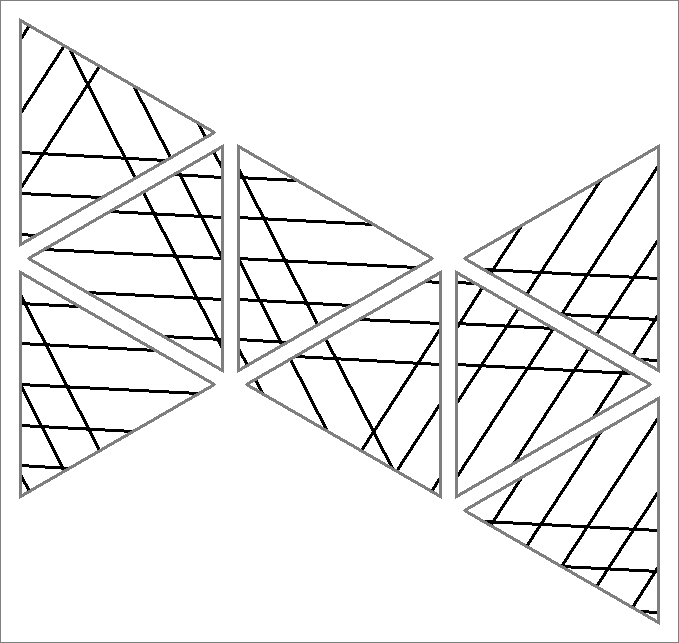 | | Same as Cube-45A
and Icosahedron-45B | | 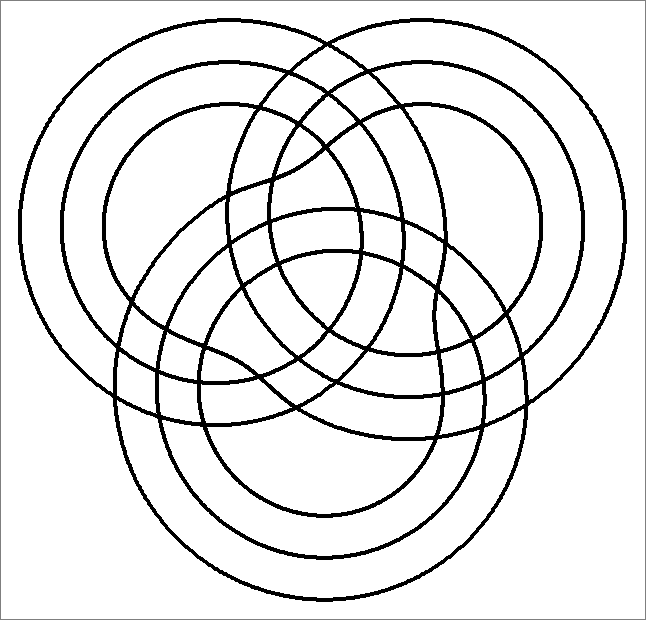 |
| 45D | | 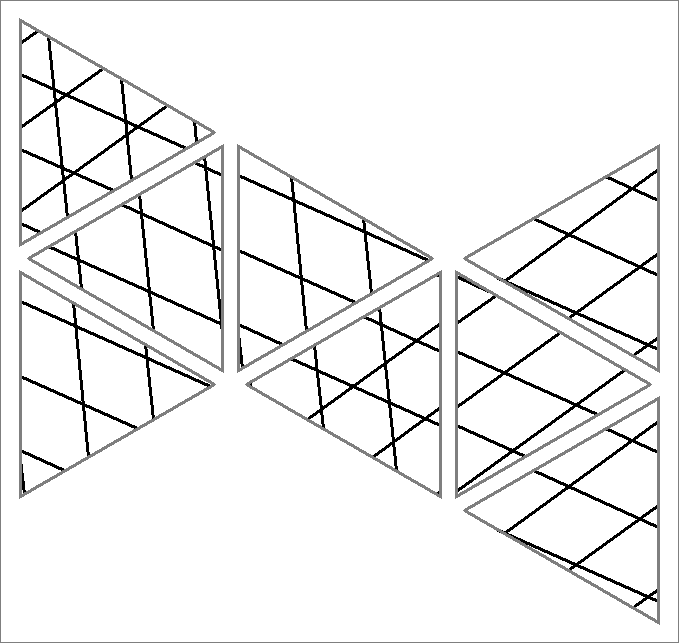 | | | | |
| 45E | | 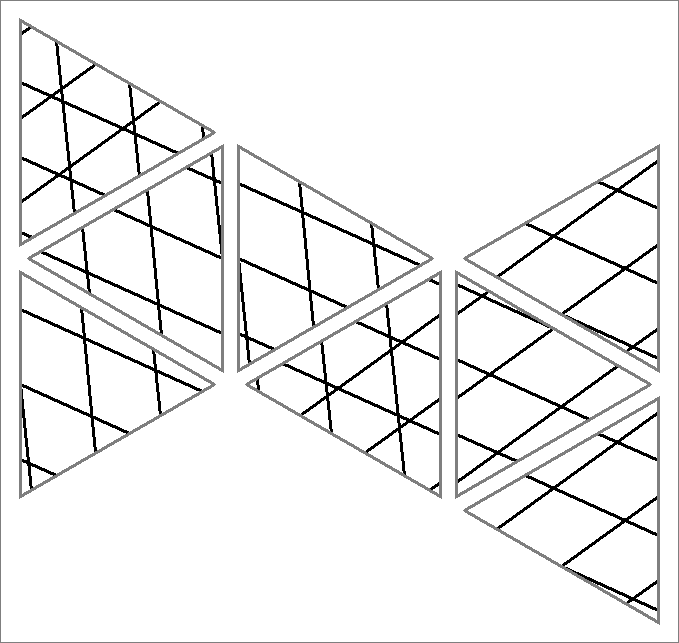 | | | | |
| 46x | | 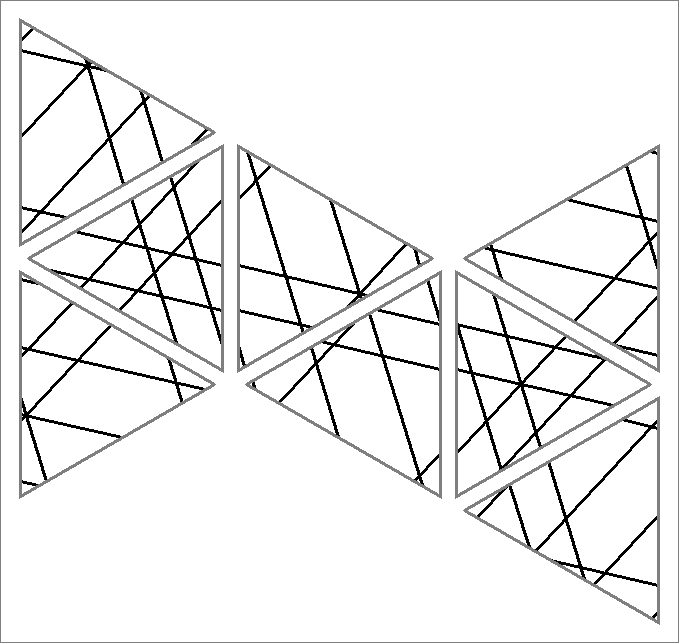 | | | | |
| 48 | | 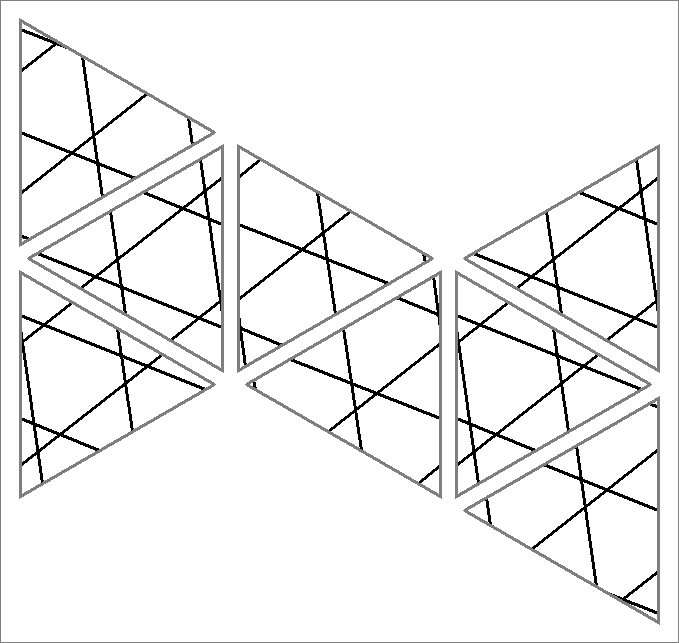 | | Contains
double edges | | |
| 51x | | 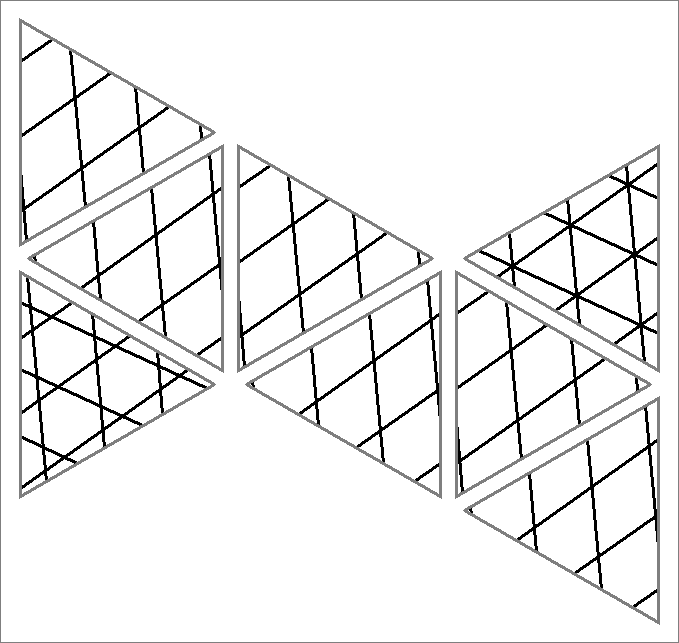 | | Contains
double edges | | |
| 54A | |  | | | | |
| 54B | |  | | | | |
| 57x | | 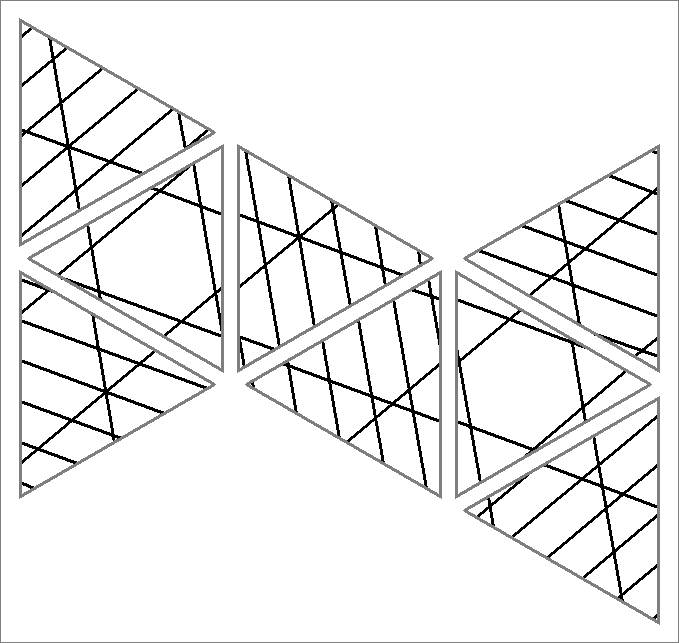 | | | | |
| 60A | | 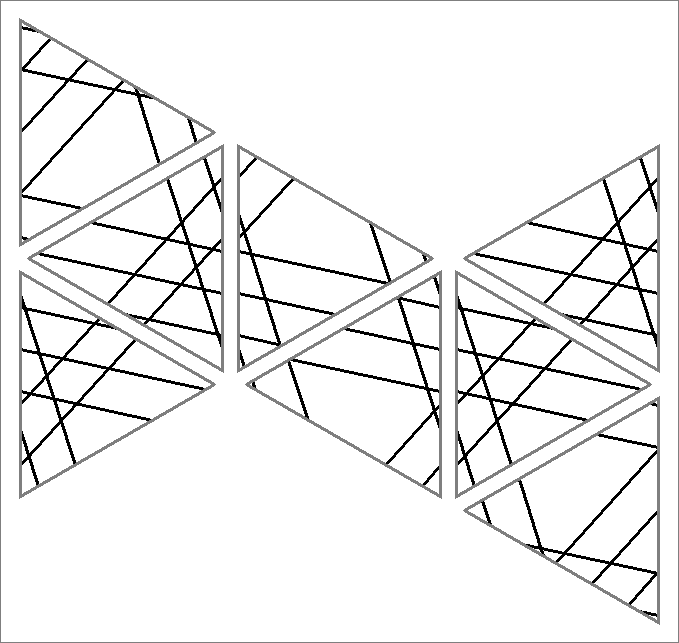 | | Contains
double edges | | |
| 60B | |  | | Contains
double edges | | |
| 60C | |  | | Contains
double edges
Same as Cube-60B
and Icosahedron-60 | |  |
| 60x | |  | | | | |
| 63A | | 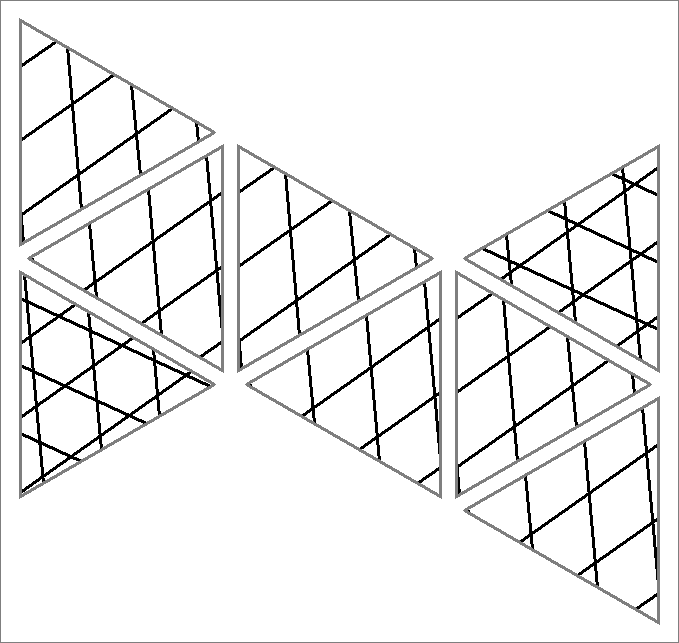 | | Contains
double edges | | |
| 63B | | 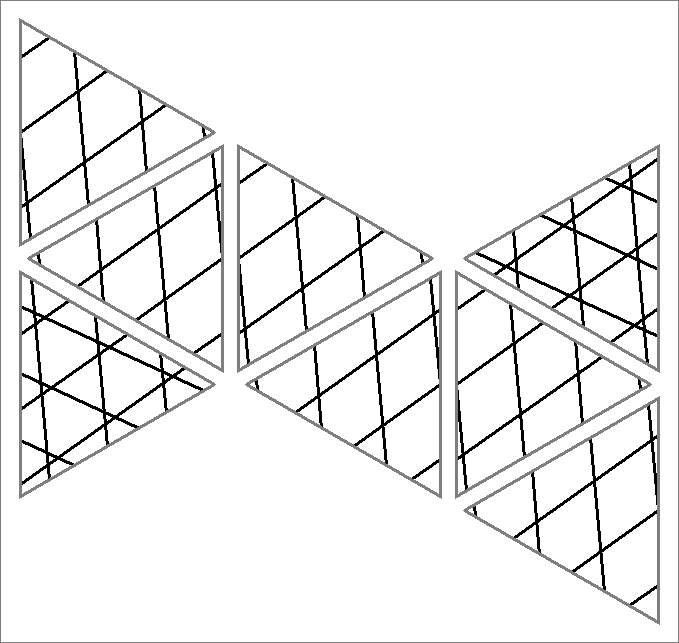 | | Contains
double edges | | |
| 63C | | 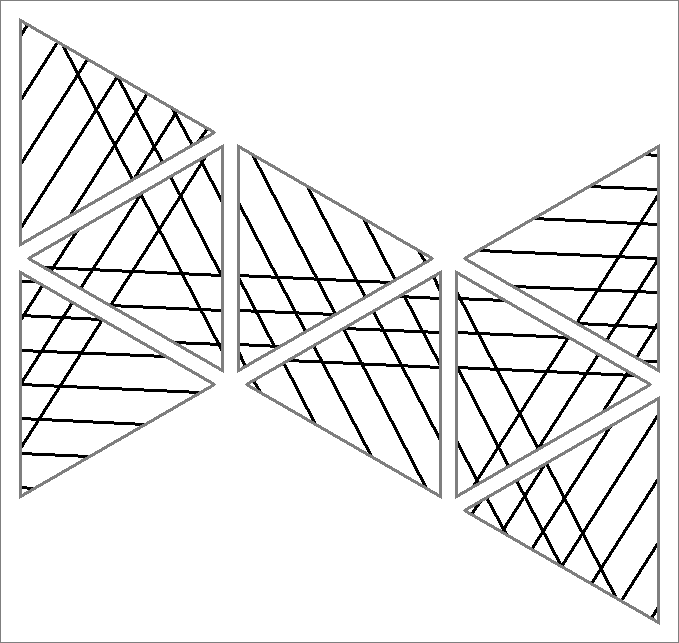 | | Same as Cube-63B
and Icosahedron-63C | | 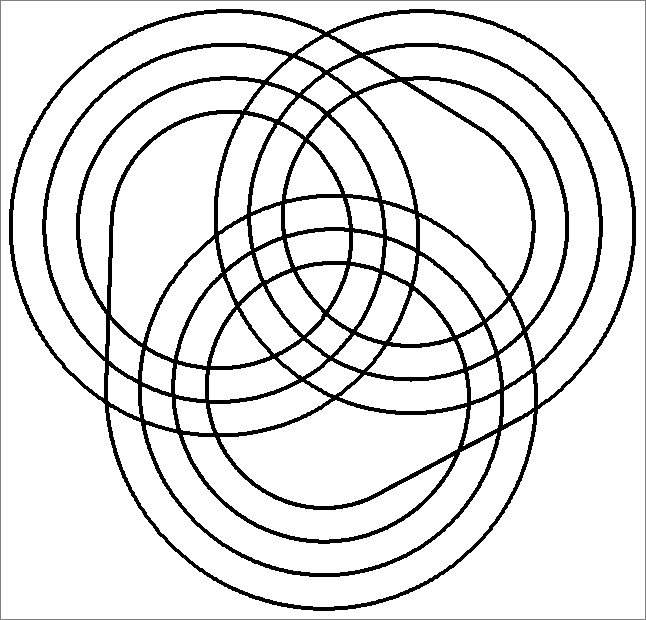 |
| 63D | | 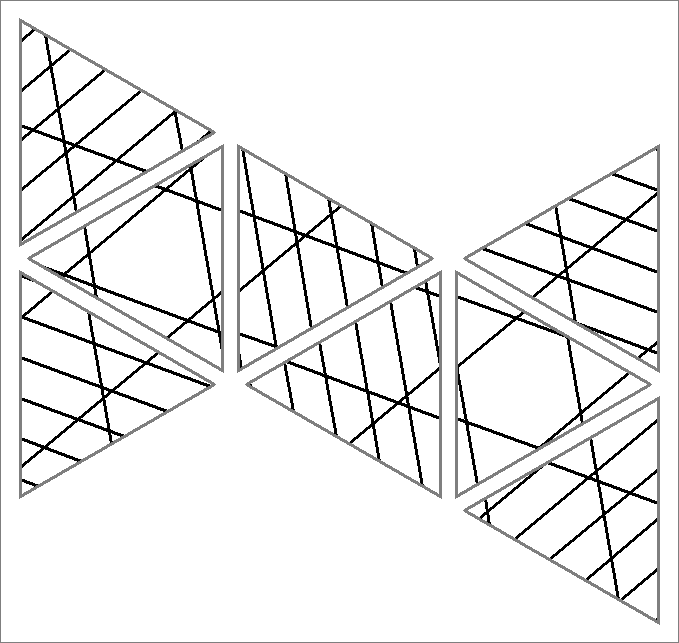 | | | | |
| 63E | | 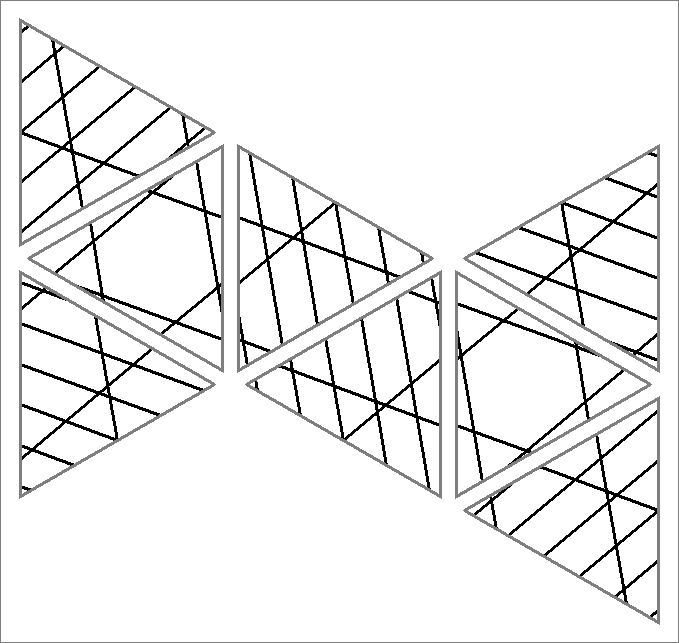 | | | | |
| 67x | | 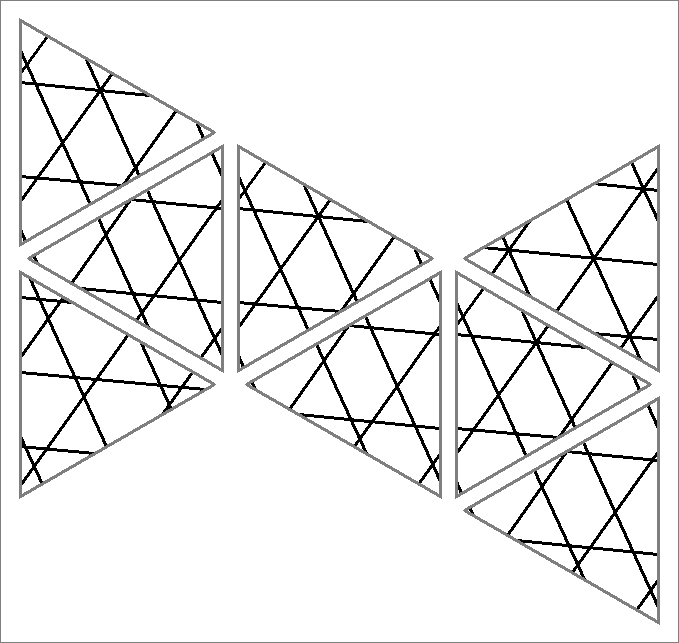 | | Contains
double edges | | |
| 72A | | 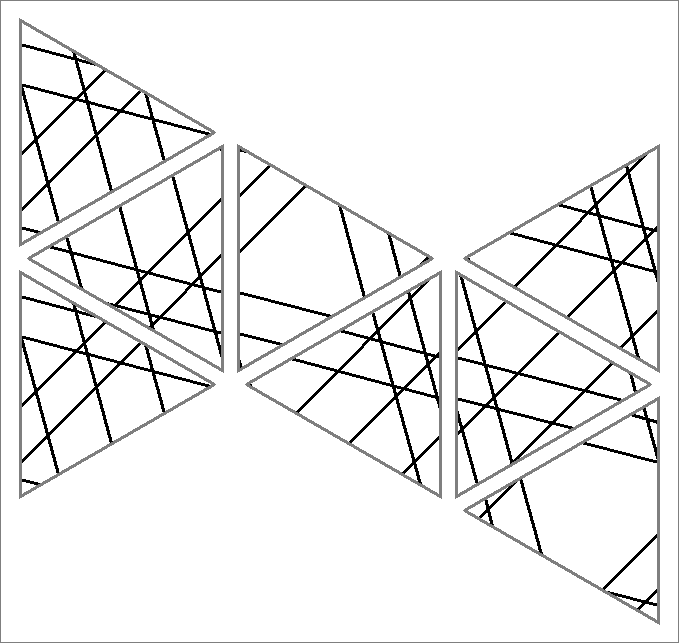 | | | | |
| 72B | | 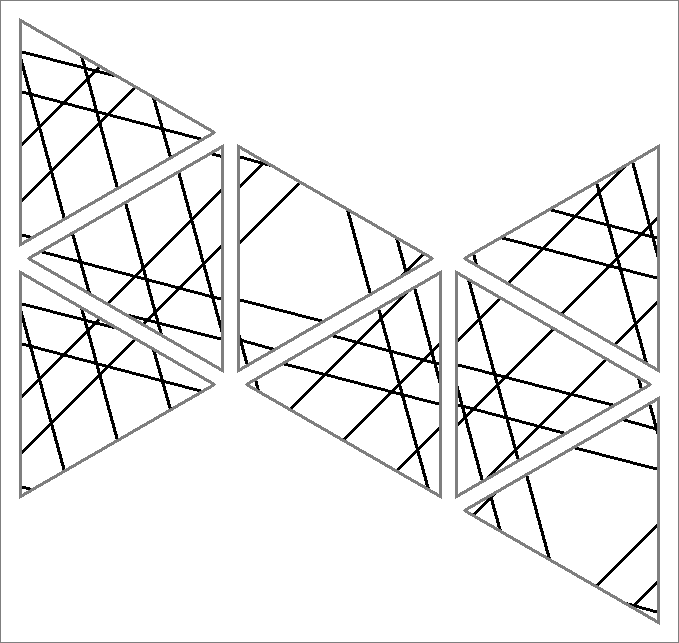 | | | | |
| 72C | | 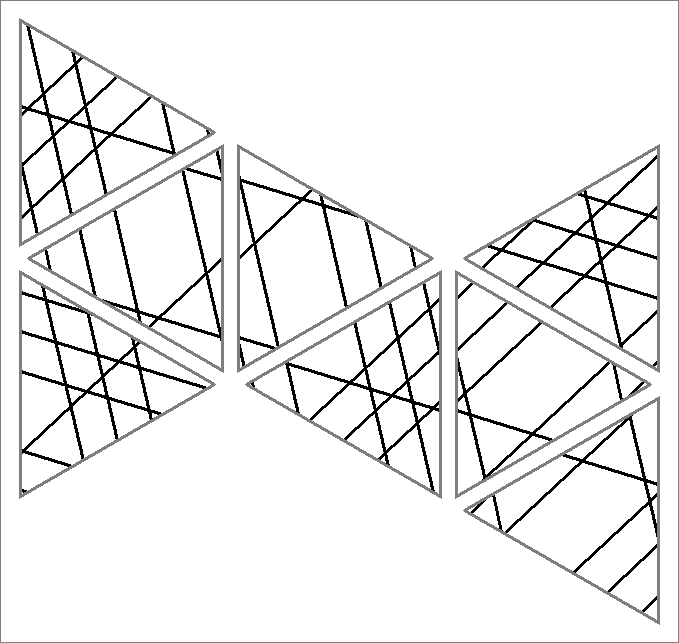 | | Contains
double edges | | |
| 72x | |  | | | | |
| 81A | | 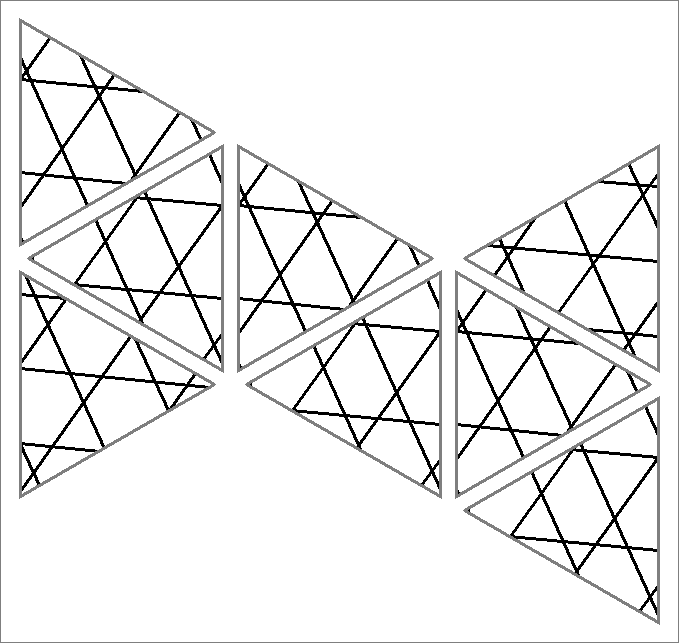 | | Contains
double edges | | |
| 81B | | 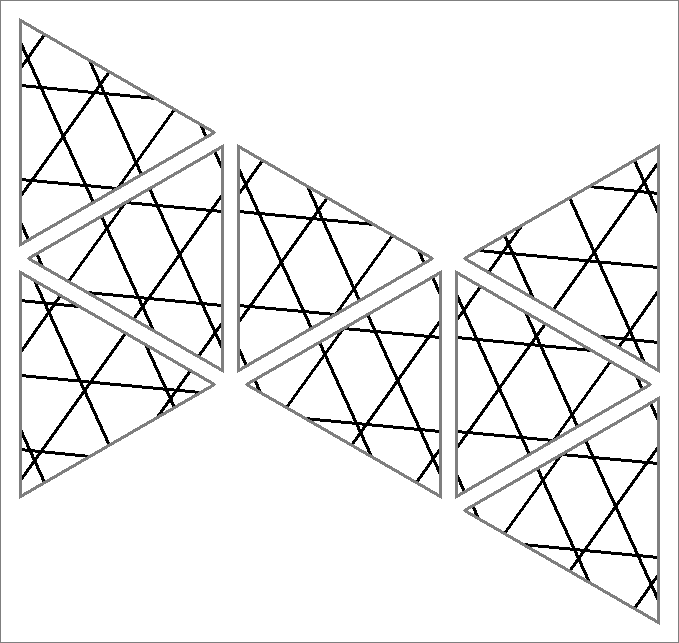 | | Contains
double edges | | |
| 81x | | 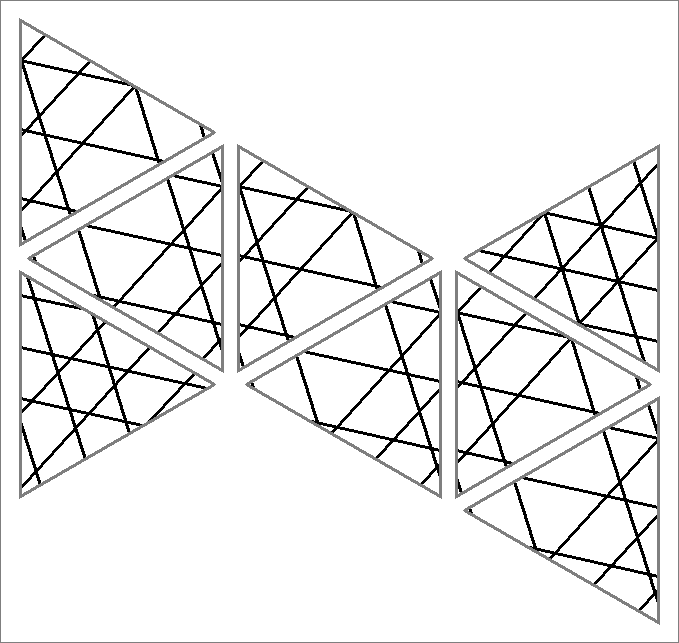 | | Contains
double edges | | |
| 84A | | 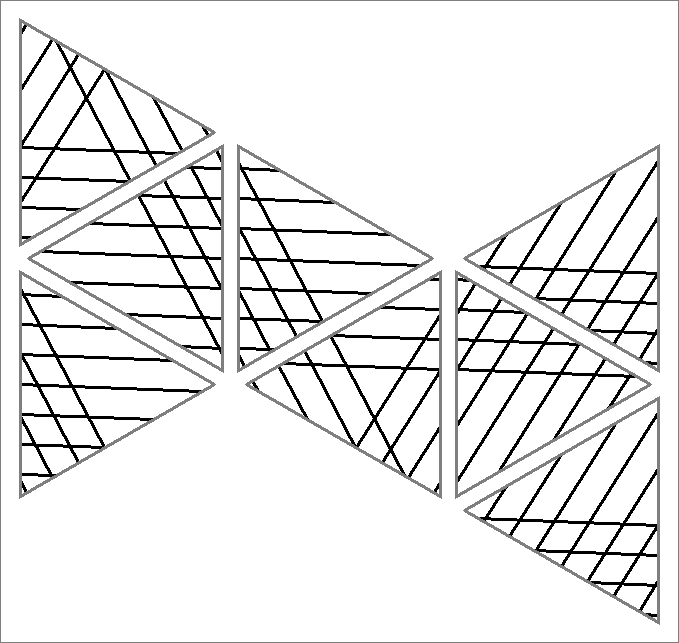 | | Same as Cube-84A
and Icosahedron-84A | | 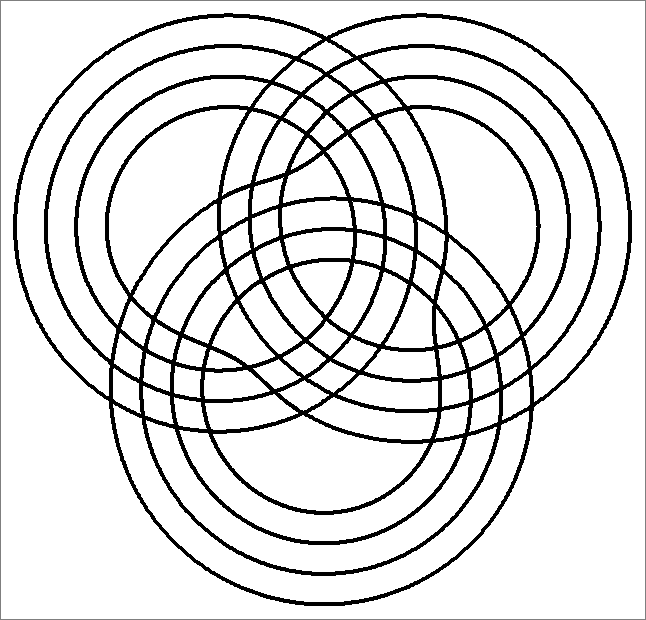 |
| 84B | | 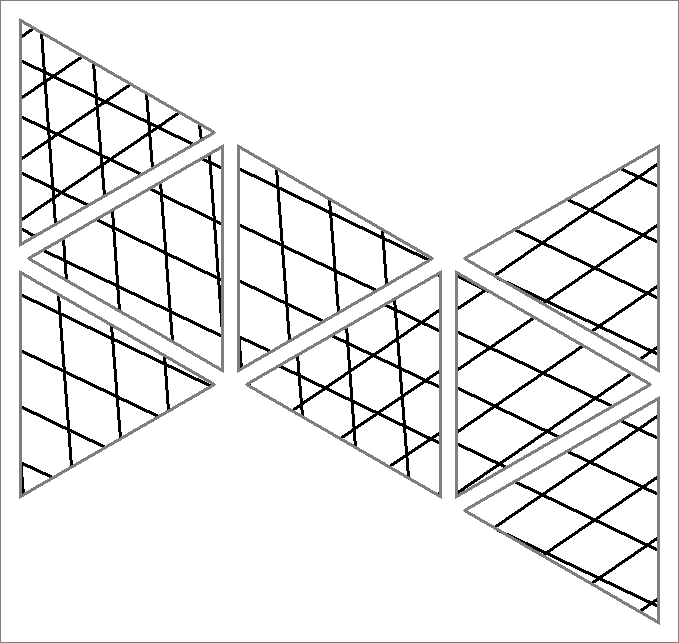 | | | | |
| 84C | | 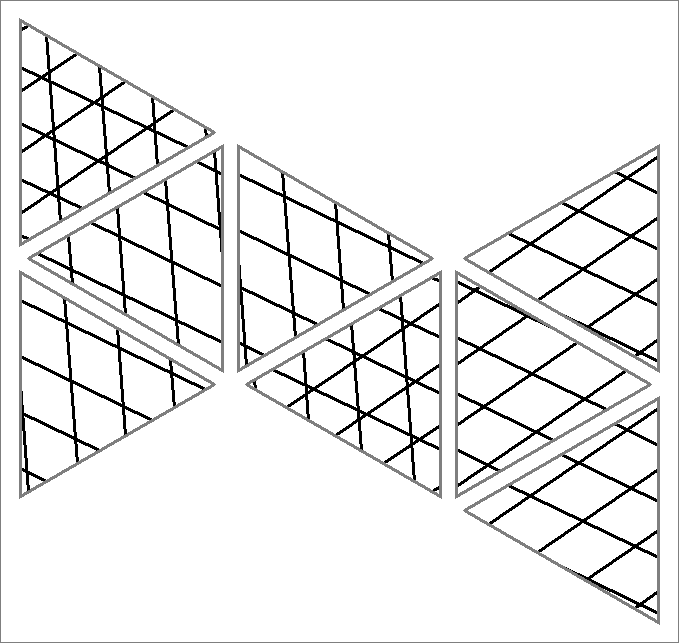 | | | | |
| 84D | | 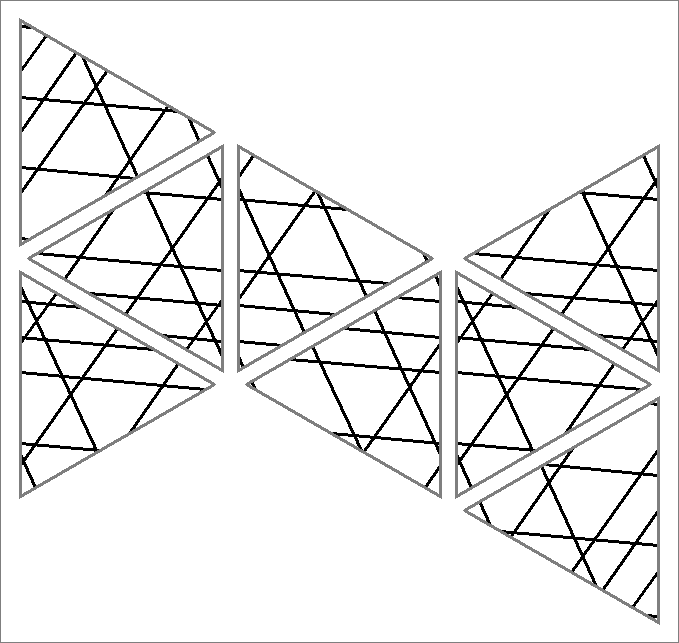 | | Contains
double edges | | |
| 84E | | 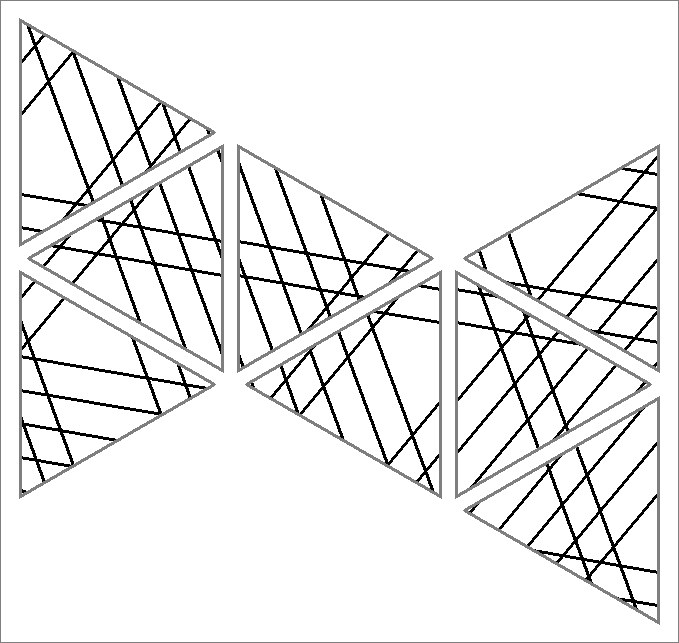 | | Contains
double edges | | |
| 84F | | 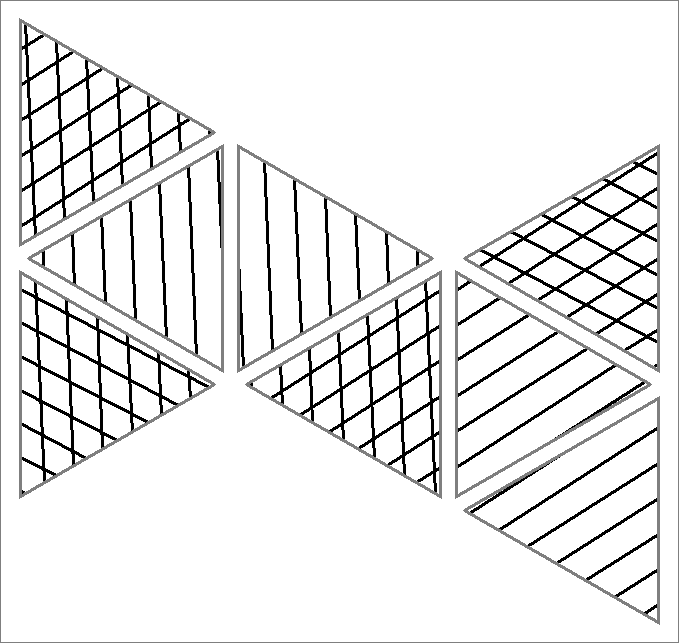 | | Contains
double edges
Same as Cube-84C
and Icosahedron-84B | | 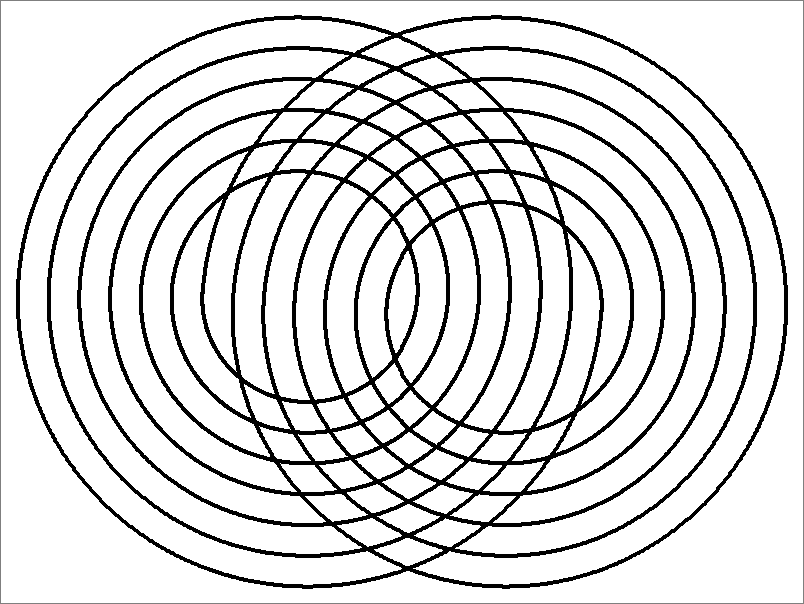 |
| 84x | | 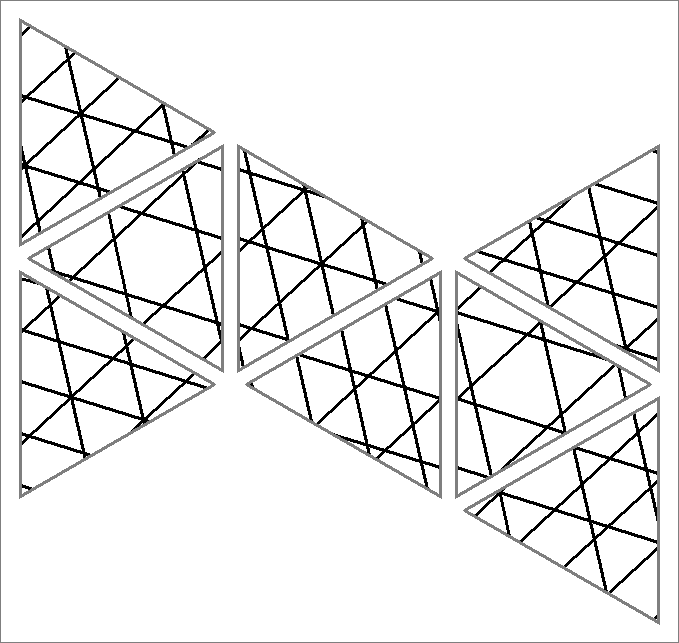 | | Contains
double edges | | |
| 87x | |  | | | | |
| 88x | | 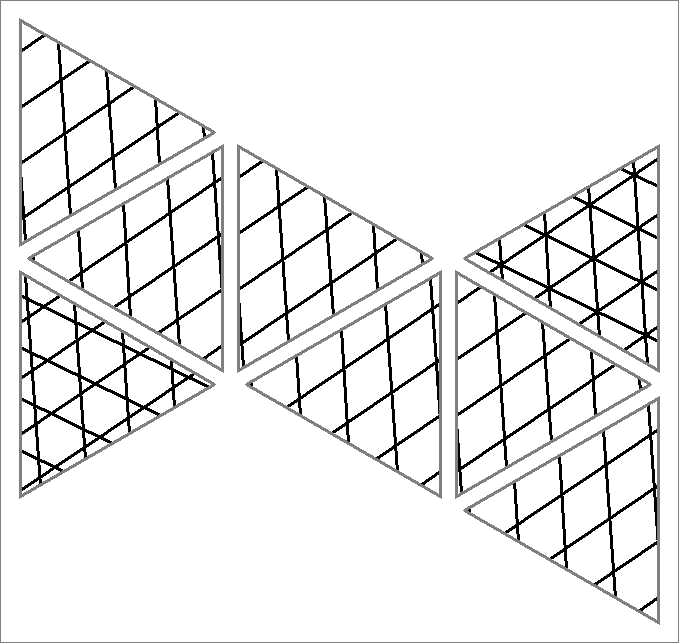 | | Contains
double edges | | |
| 94x | | 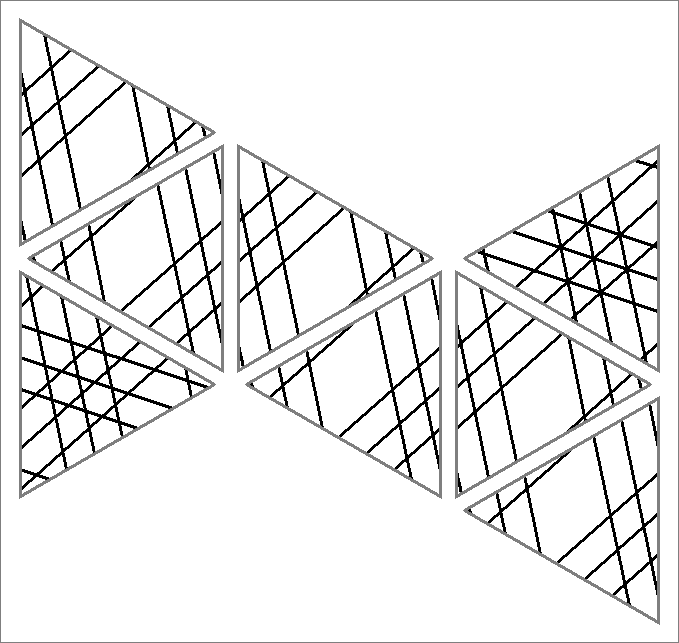 | | | | |
| 96 | | 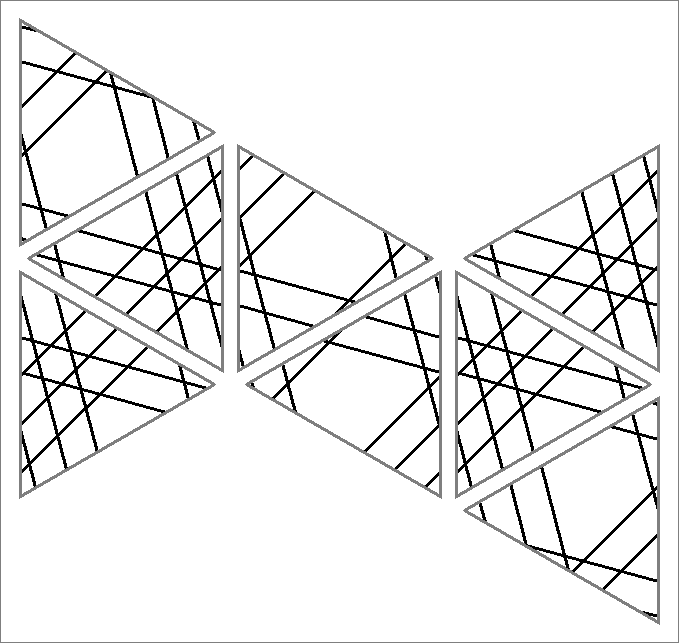 | | Contains
double edges | | |
| 99A | | 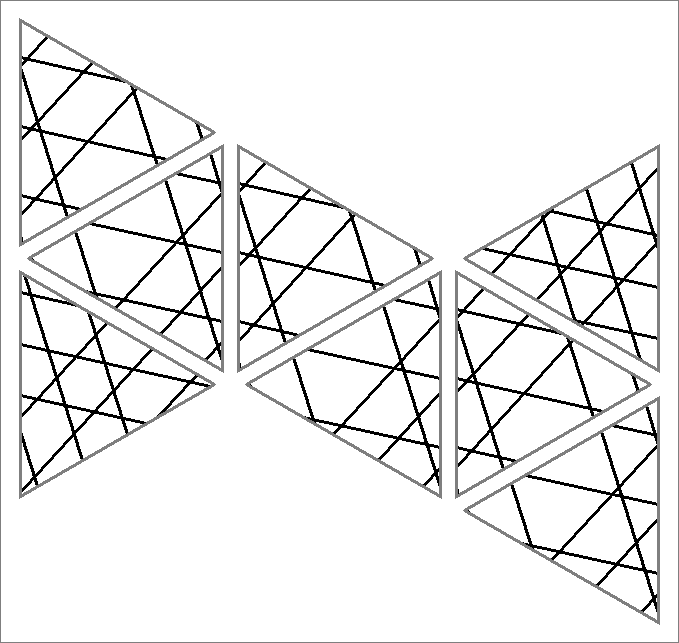 | | Contains
double edges | | |
| 99B | |  | | Contains
double edges | | |
| 99C | | 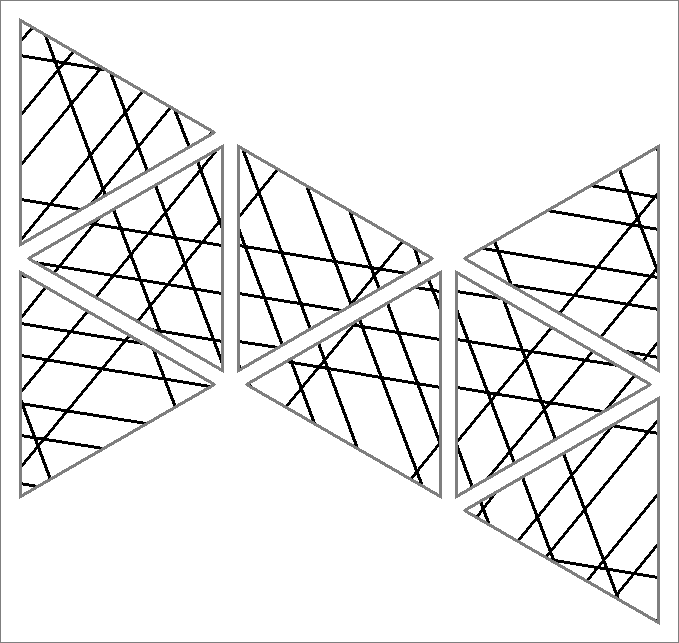 | | | | |
| 99D | |  | | | | |
| 102A | | 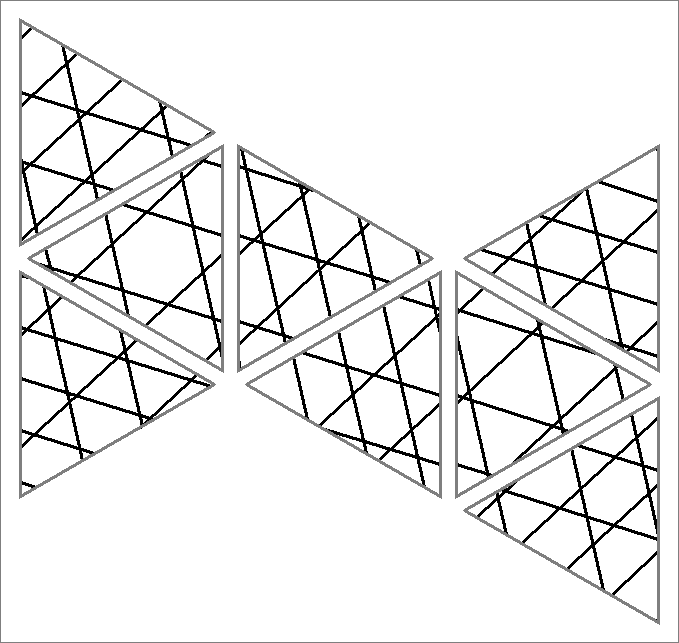 | | Contains
double edges | | |
| 102B | | 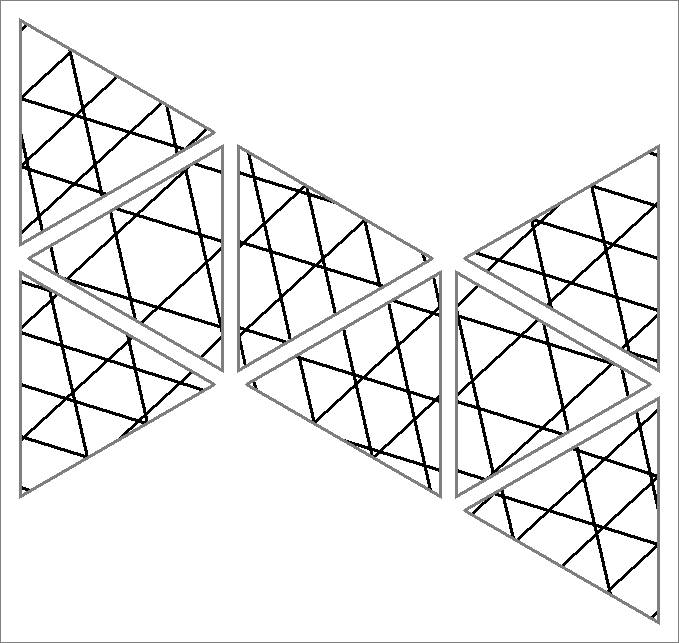 | | Contains
double edges | | |
| 108A | | 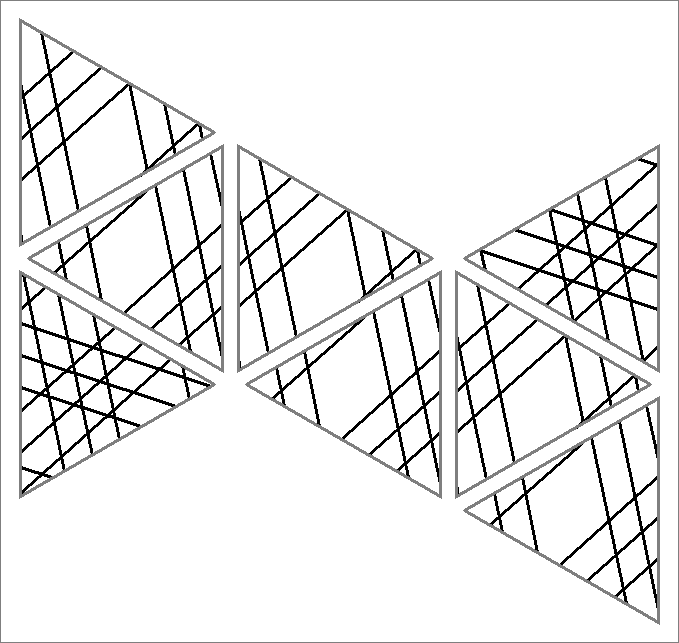 | | | | |
| 108B | |  | | | | |
| 108C | | 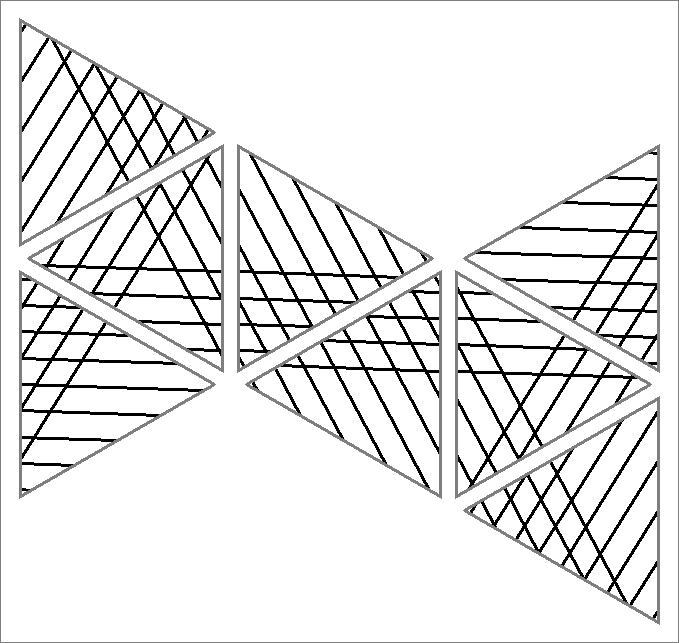 | | Same as Cube-108A
and Icosahedron-108A | | 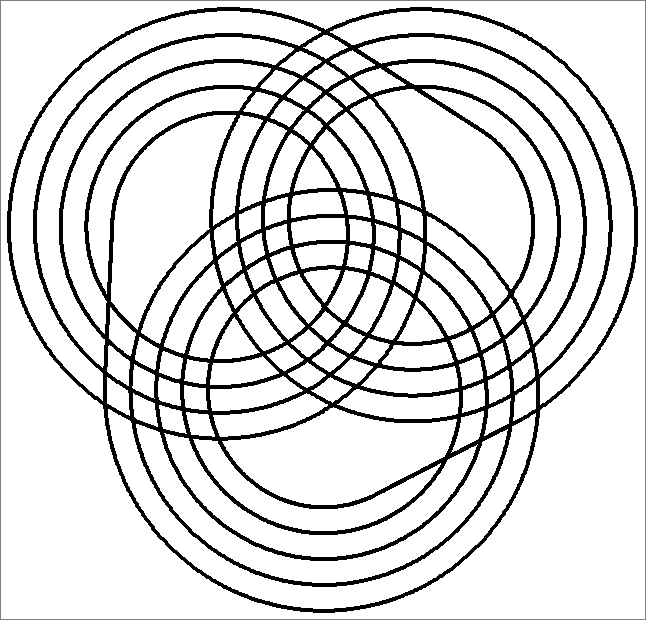 |
| 108D | |  | | Contains
double edges | | |
| 108E | | 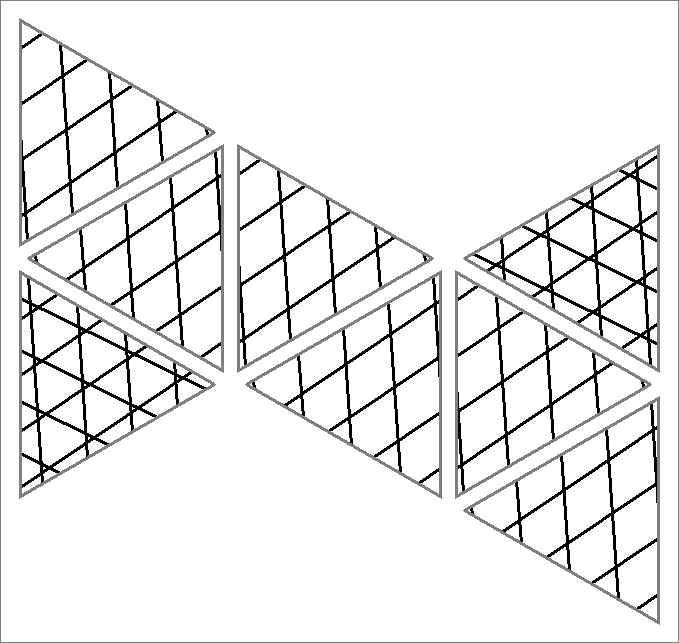 | | Contains
double edges | | |
| 108F | |  | | Contains
double edges | | |
| 111x | | 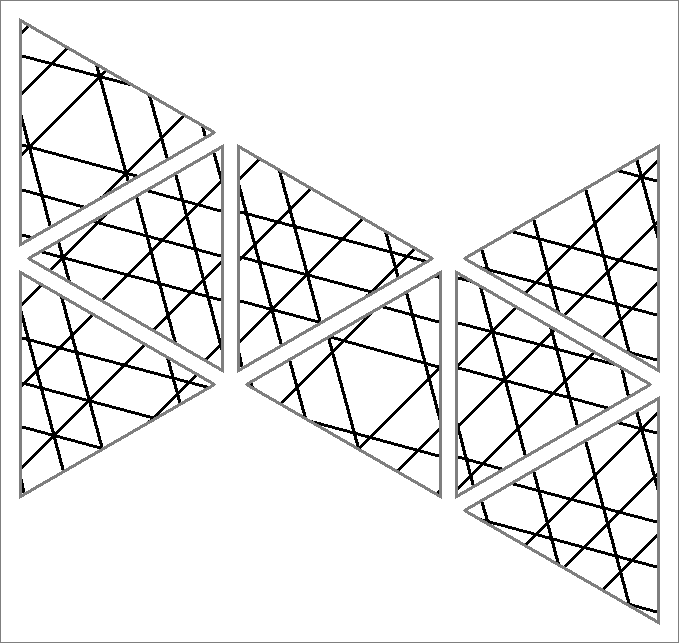 | | Contains
double edges | | |
| 112A | | 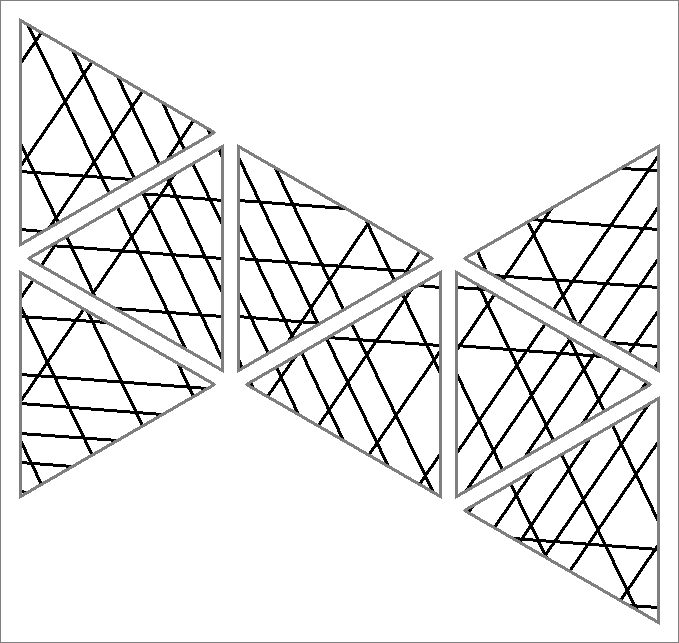 | | Contains
double edges | | |
| 112B | | 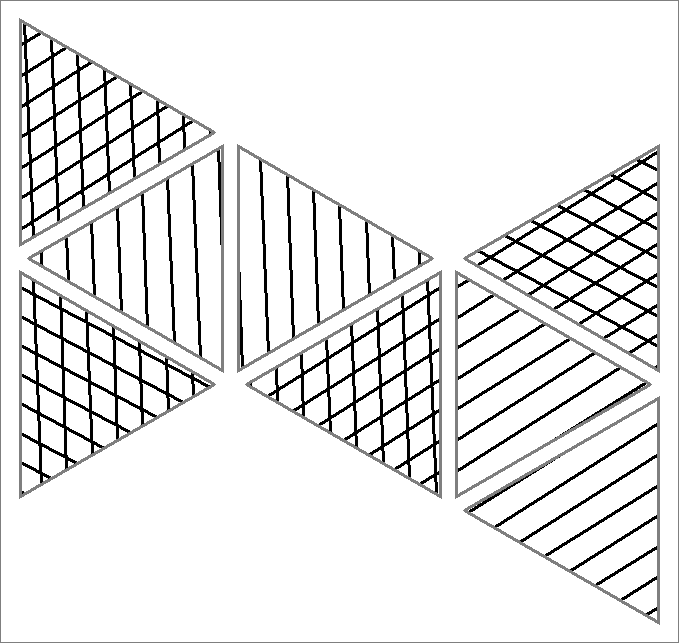 | | Contains
double edges
Same as Cube-112B
and Icosahedron-112B | | 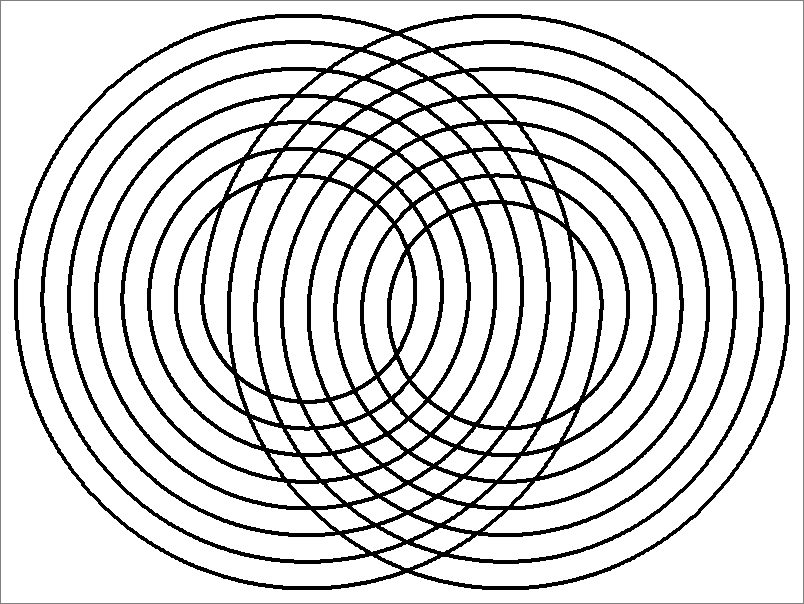 |
| 115x | | 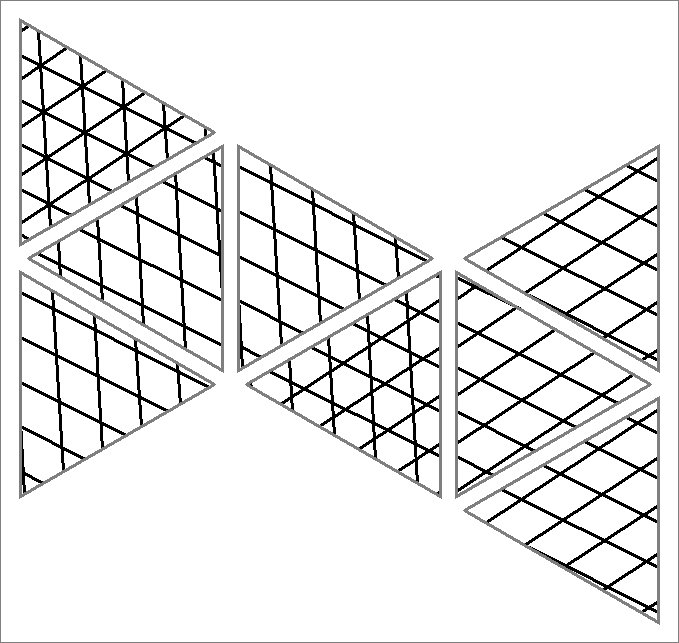 | | | | |
| 117x | |  | | | | |
| 120x | | 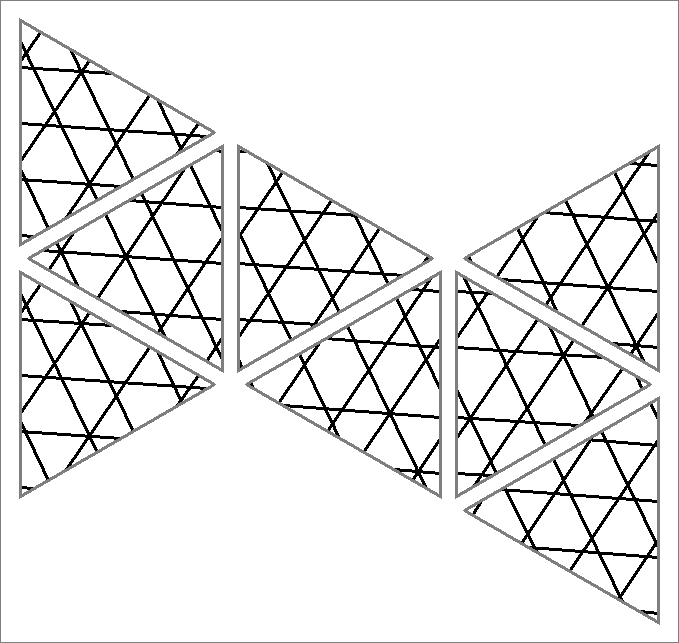 | | Contains
double edges | | |
| 121x | | 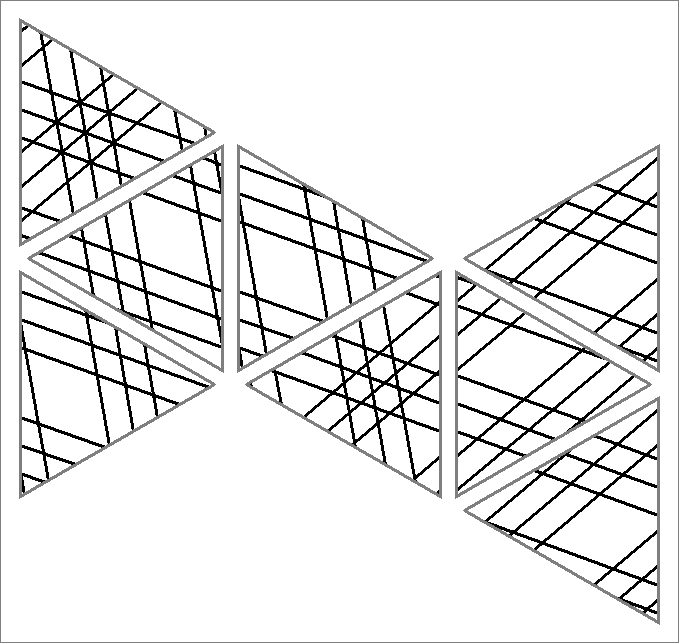 | | | | |
| 132A | | 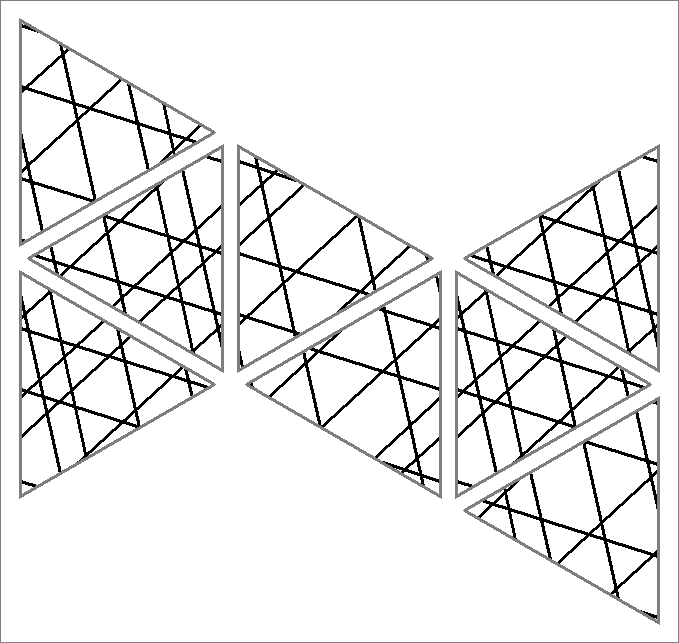 | | Contains
double edges | | |
| 132B | | 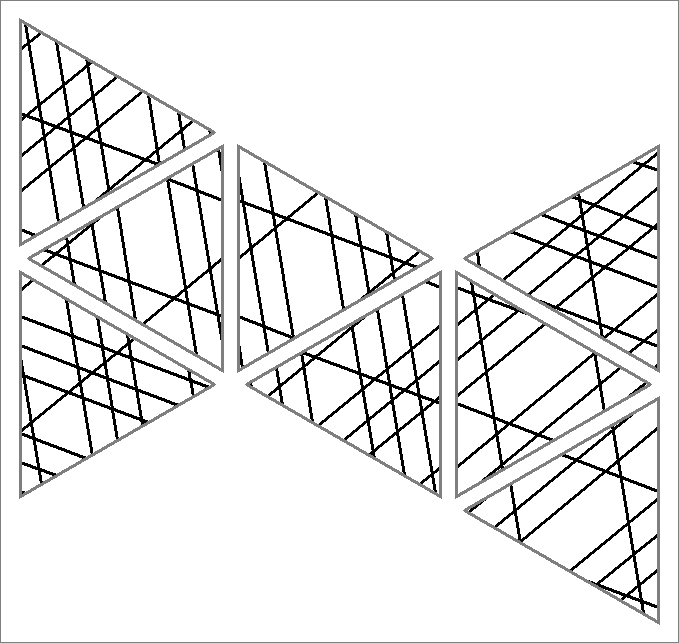 | | Contains
double edges | | |
| 135A | | 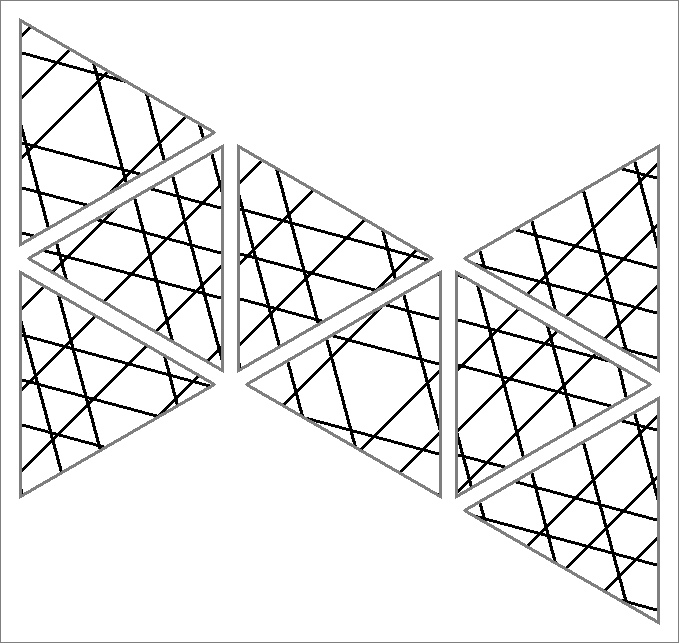 | | Contains
double edges | | |
| 135B | |  | | Contains
double edges | | |
| 135C | | 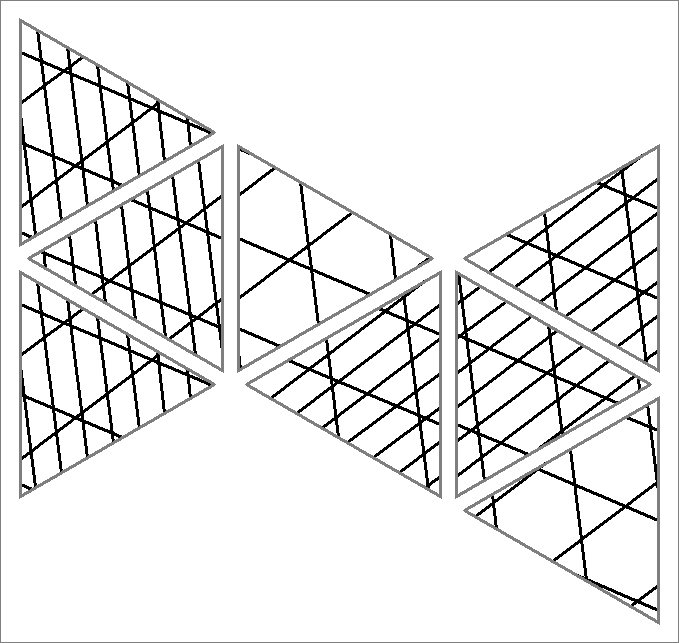 | | | | |
| 135D | | 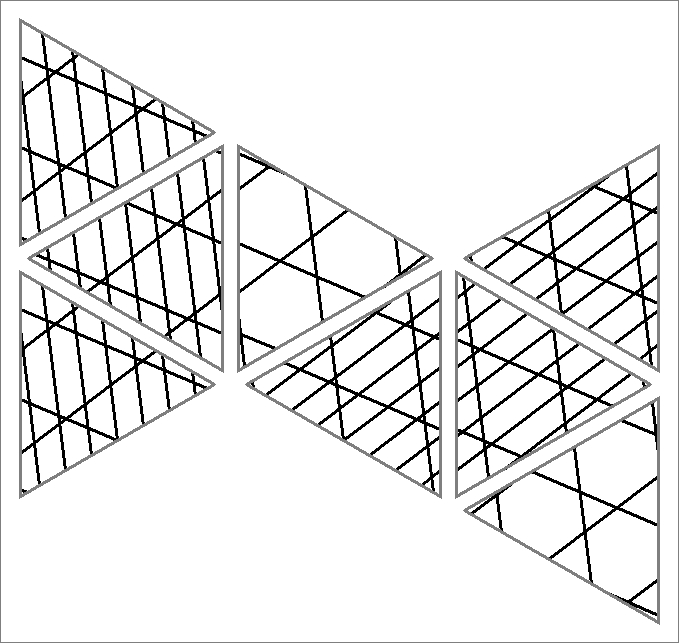 | | | | |
| 135E | | 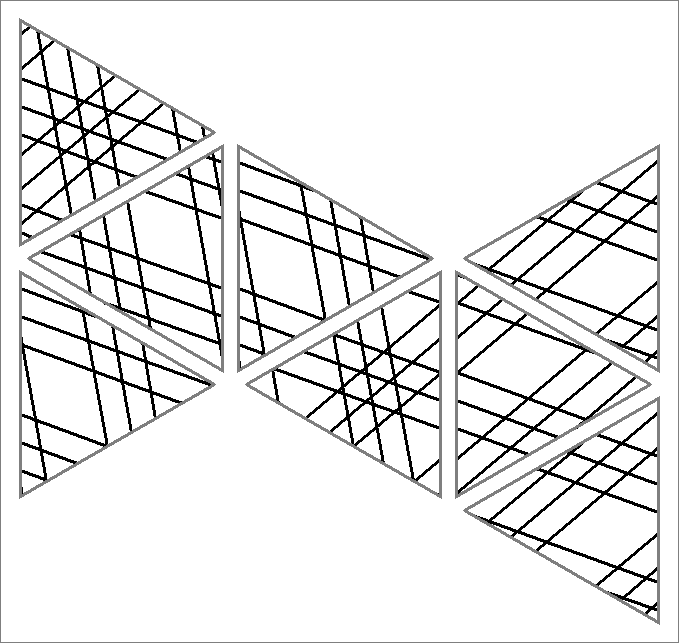 | | | | |
| 135F | | 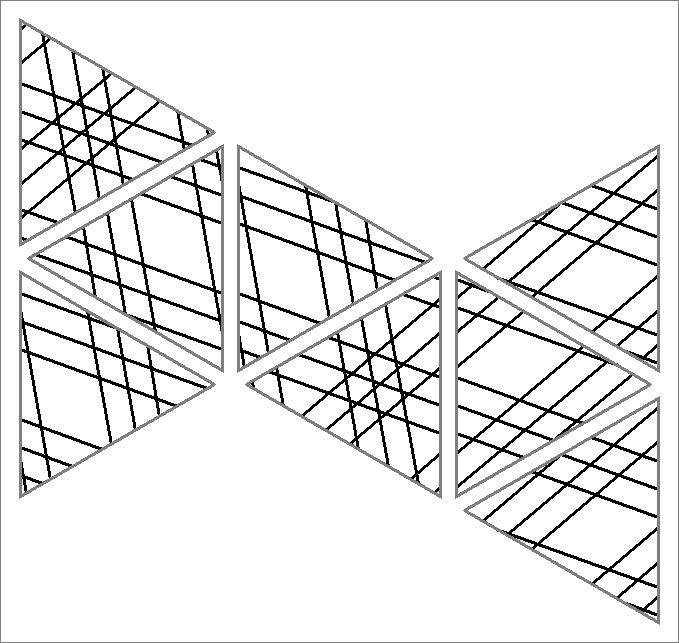 | | | | |
| 135G | | 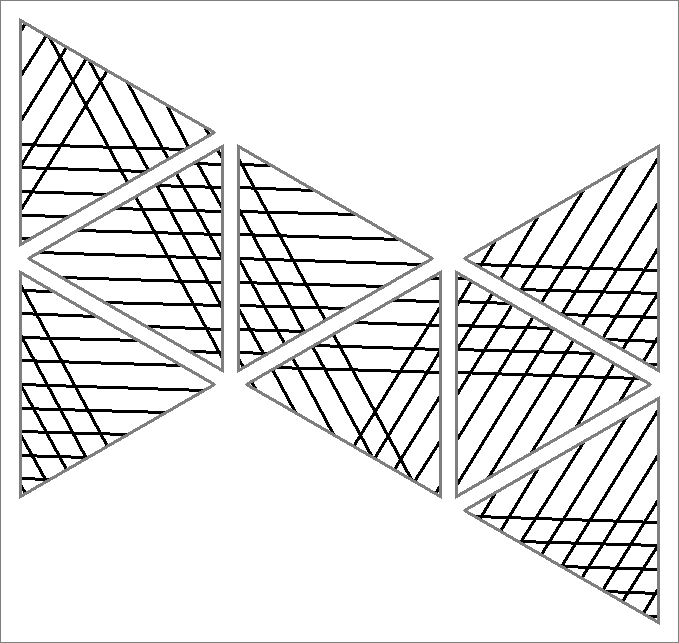 | | Same as Cube-135A
and Icosahedron-135B | | 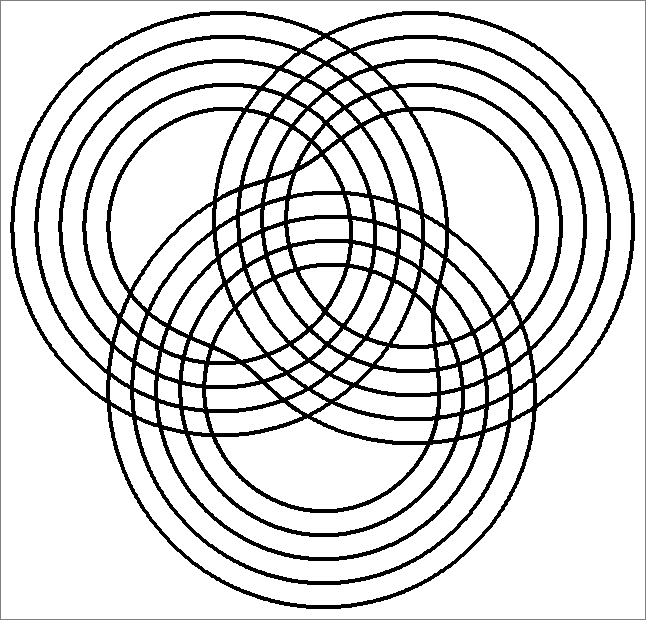 |
| 135H | | 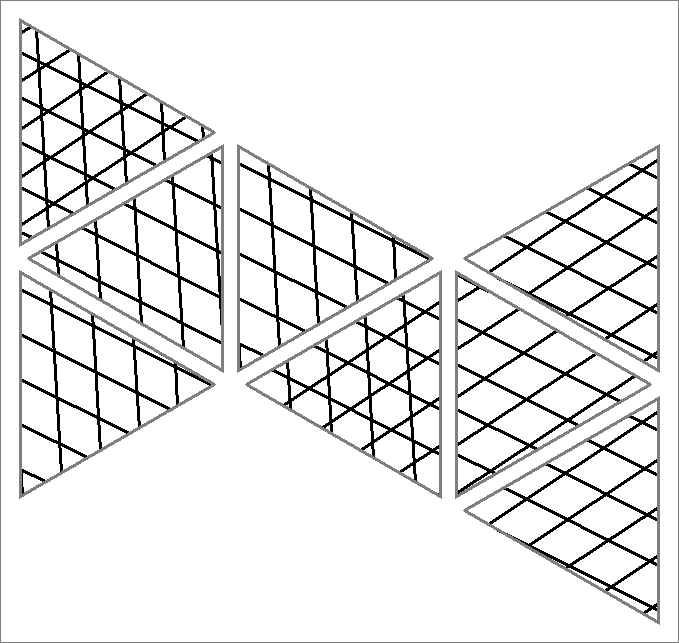 | | | | |
| 135I | |  | | | | |
| 135x | | 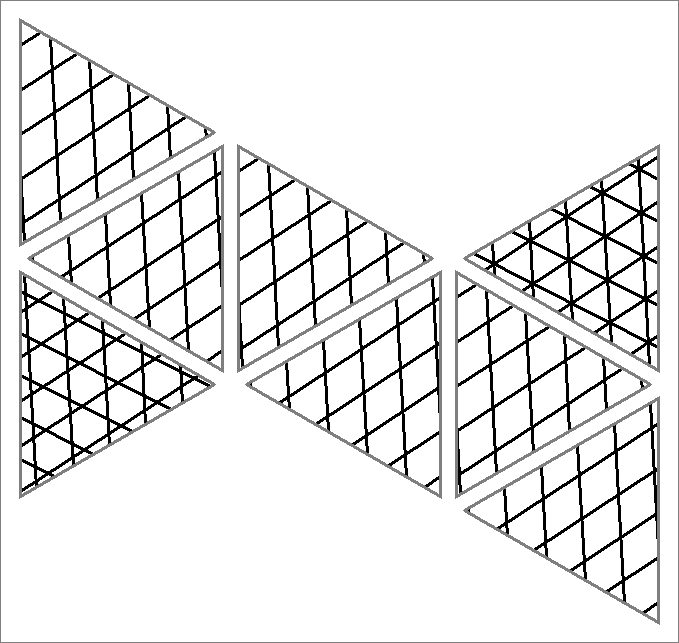 | | Contains
double edges | | |
| 136 | | 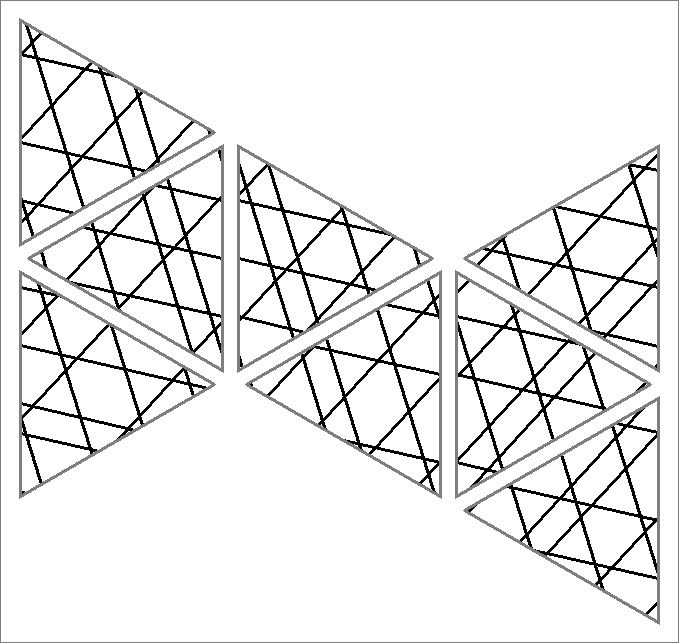 | | Contains
double edges | | |
| 136x | | 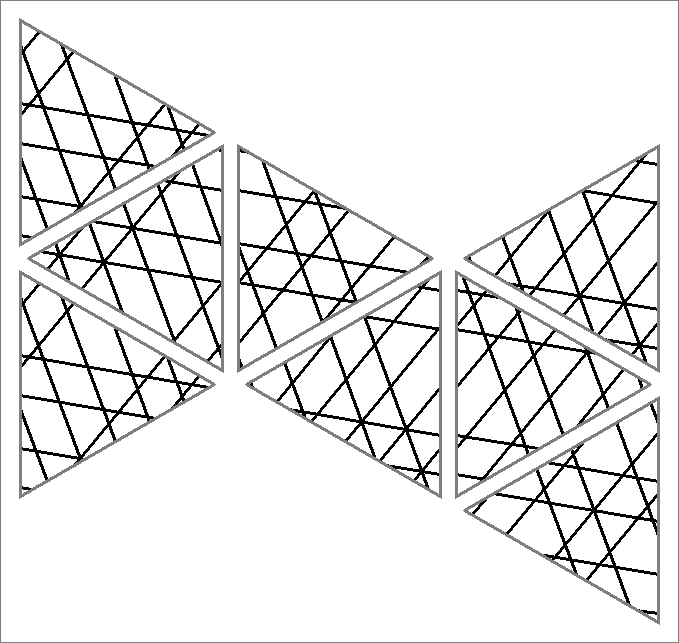 | | Contains
double edges | | |
| 138x | |  | | | | |
| 144A | | 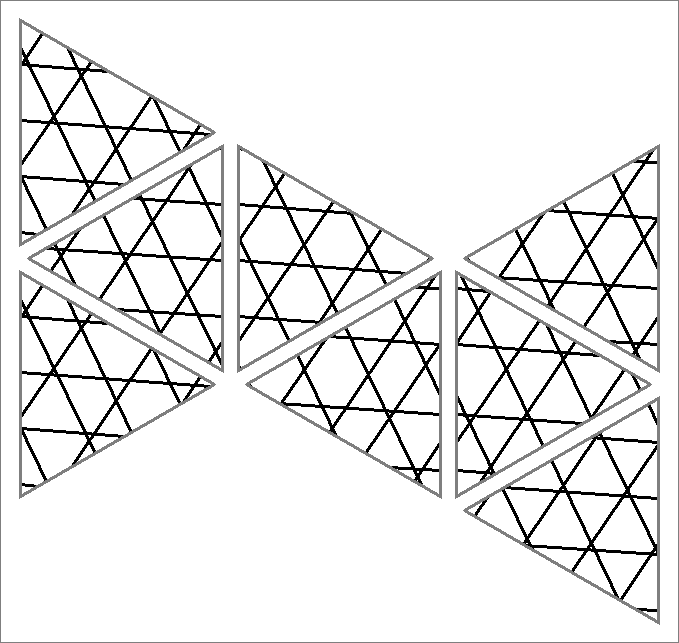 | | Contains
double edges | | |
| 144B | |  | | Contains
double edges | | |
| 144C | | 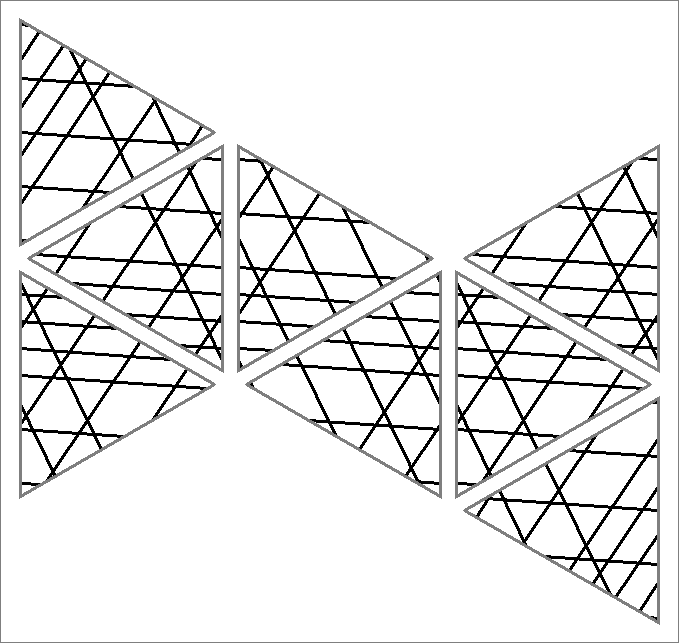 | | Contains
double edges | | |
| 144D | | 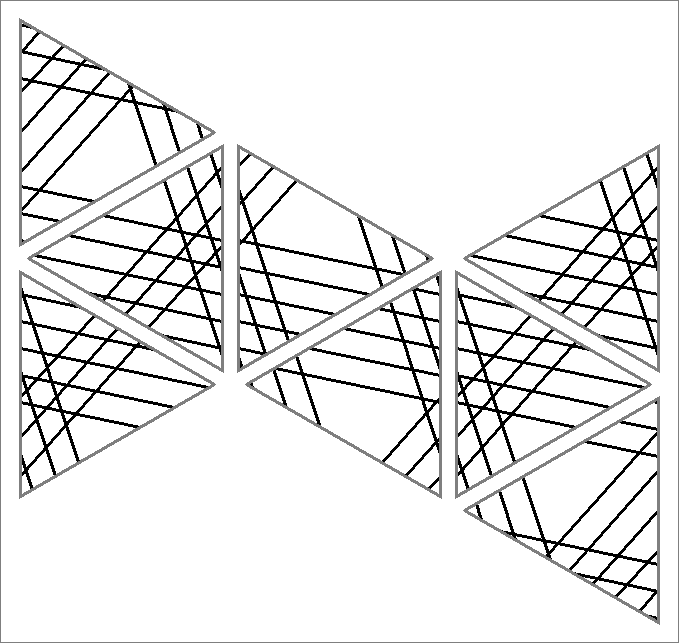 | | Contains
double edges | | |
| 144E | | 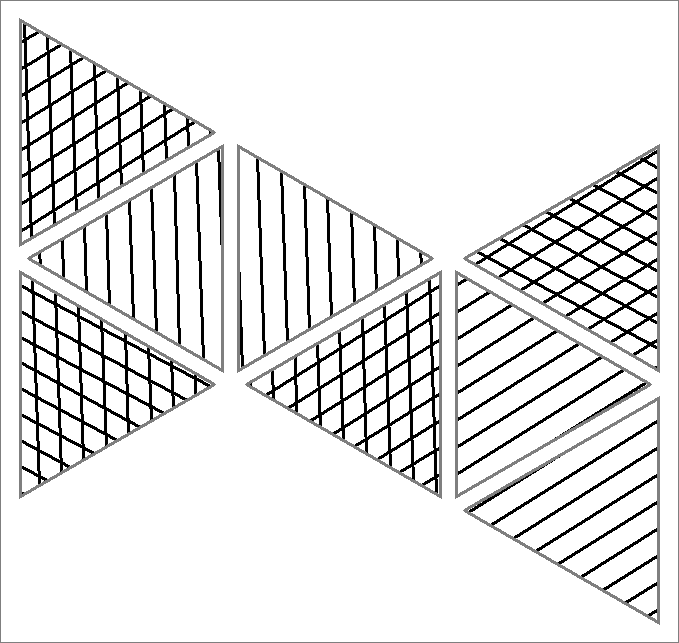 | | Contains
double edges
Same as Cube-144D
and Icosahedron-144C | | 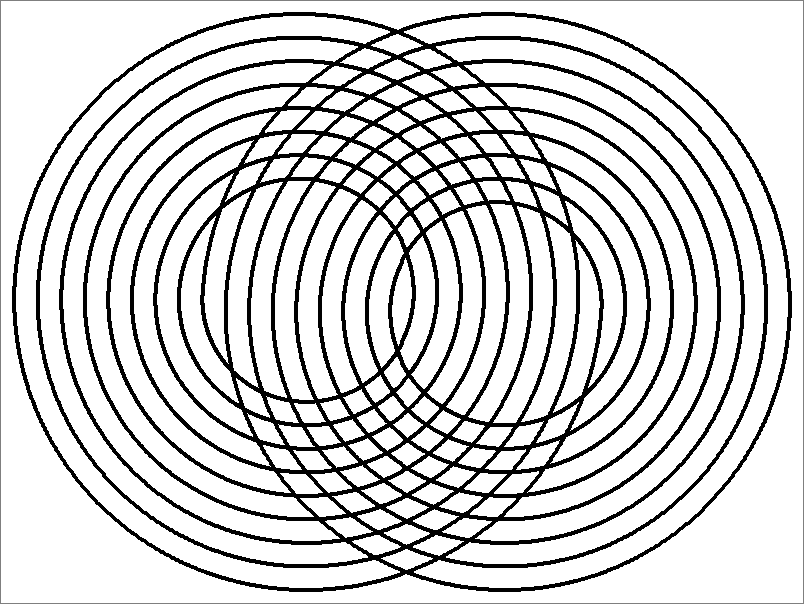 |
| 147xA | | 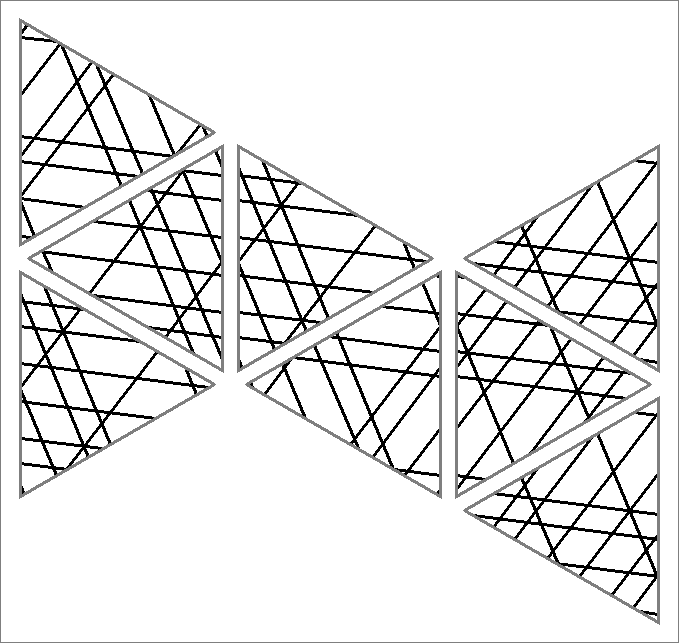 | | | | |
| 147xB | |  | | | | |
| 153x | |  | | Contains
double edges | | |
| 160x | | 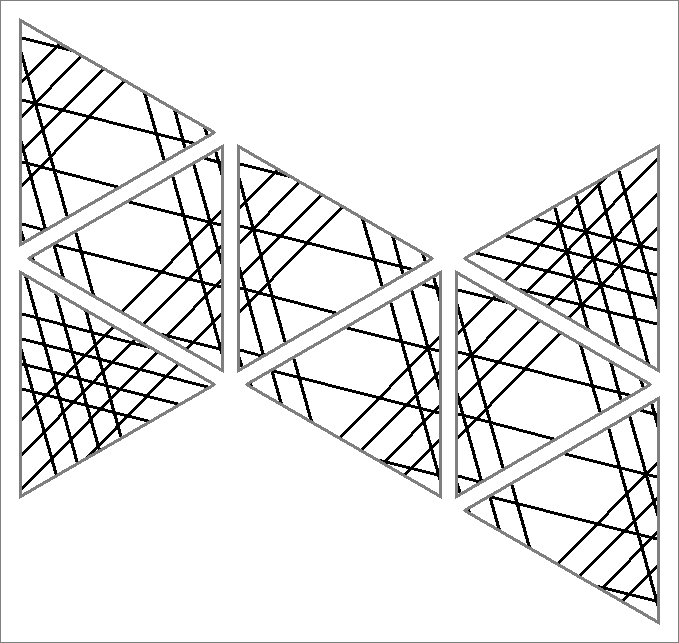 | | | | |
| 162A | |  | | Contains
double edges | | |
| 162B | |  | | Contains
double edges | | |
| 162C | |  | | | | |
| 162D | |  | | | | |
| 165A | |  | | Same as Cube-165A
and Icosahedron-165D | |  |
| 165B | |  | | Contains
double edges | | |
| 165C | | 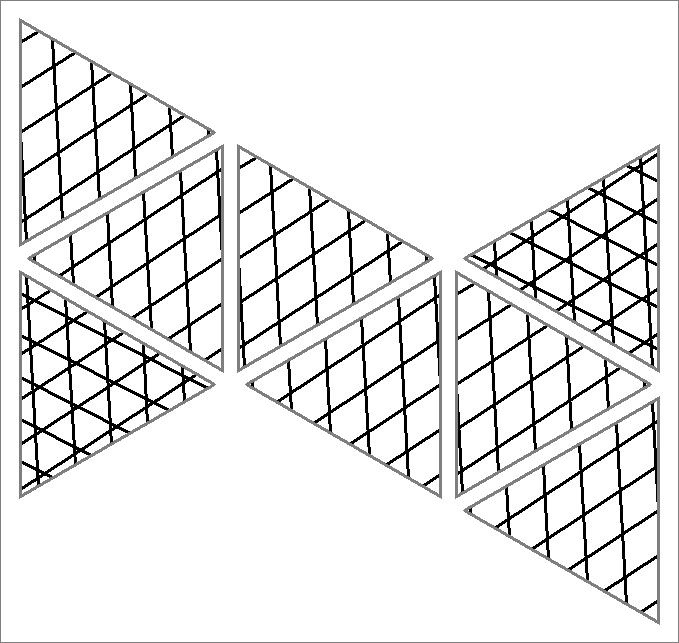 | | Contains
double edges | | |
| 165D | | 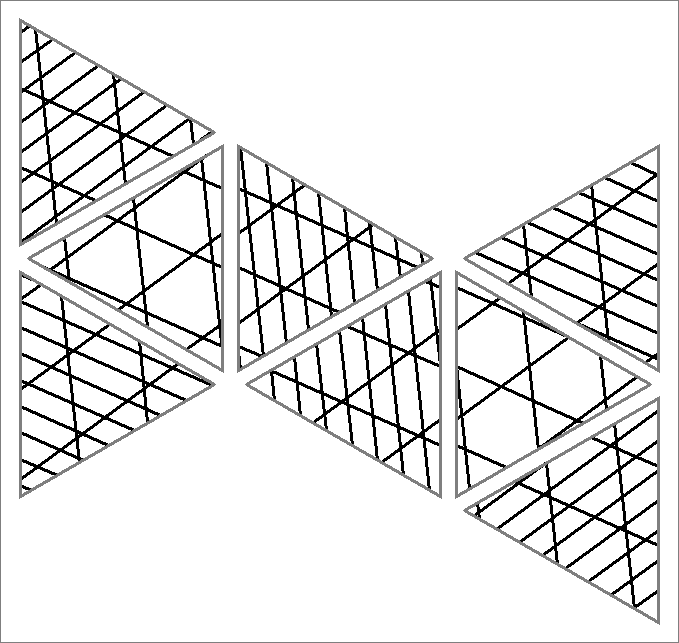 | | | | |
| 165E | | 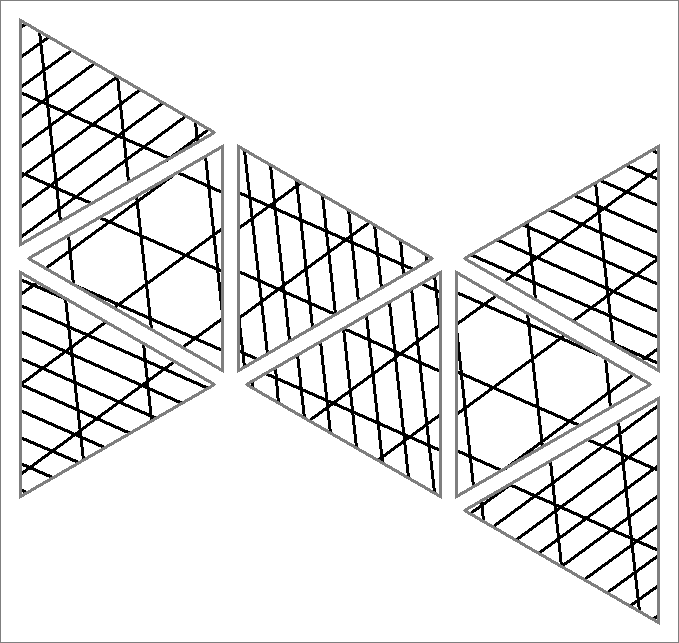 | | | | |
| 168xA | | 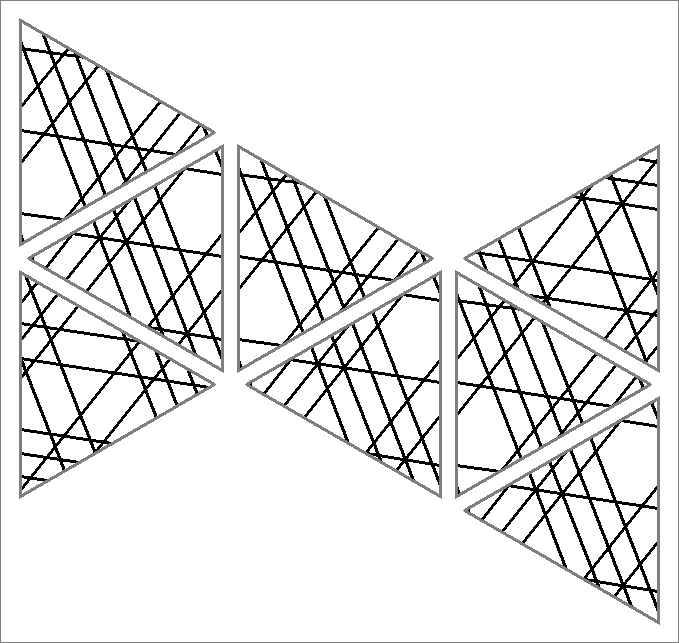 | | | | |
| 168xB | | 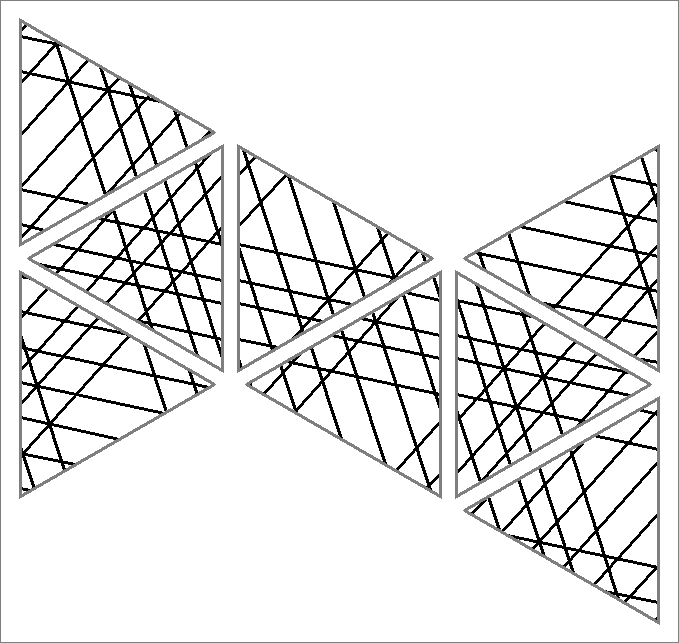 | | | | |
| 168xC | |  | | | | |
| 171A | | 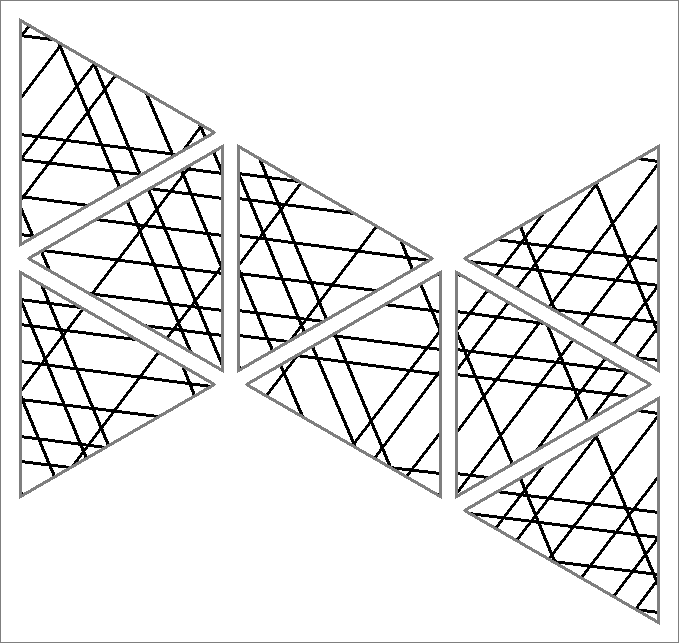 | | | | |
| 171B | | 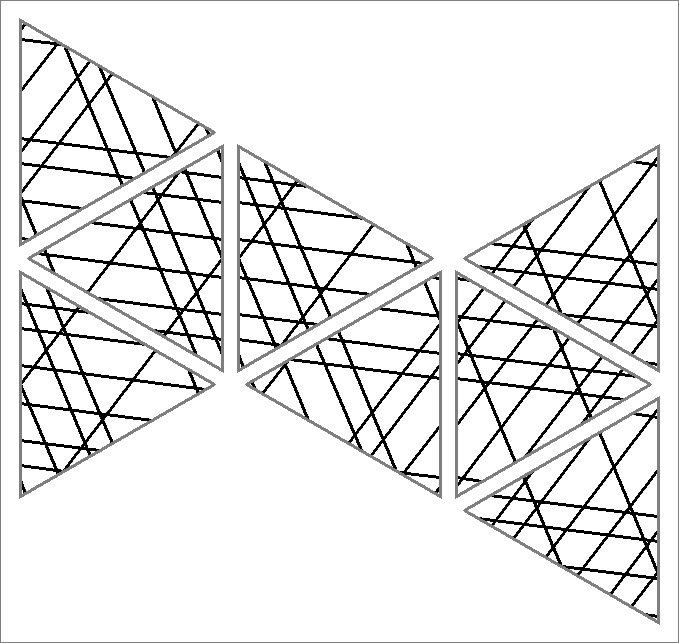 | | | | |
| 174x | | 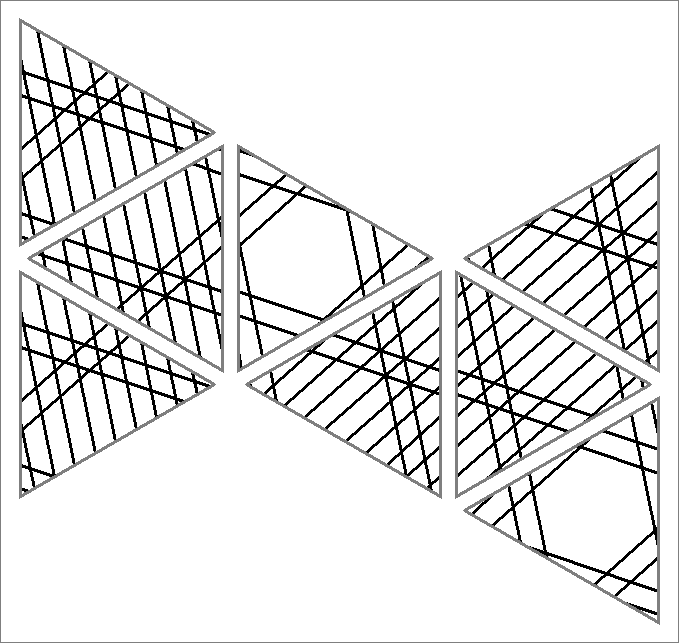 | | | | |
| 180A | |  | | Contains
double edges | | |
| 180B | | 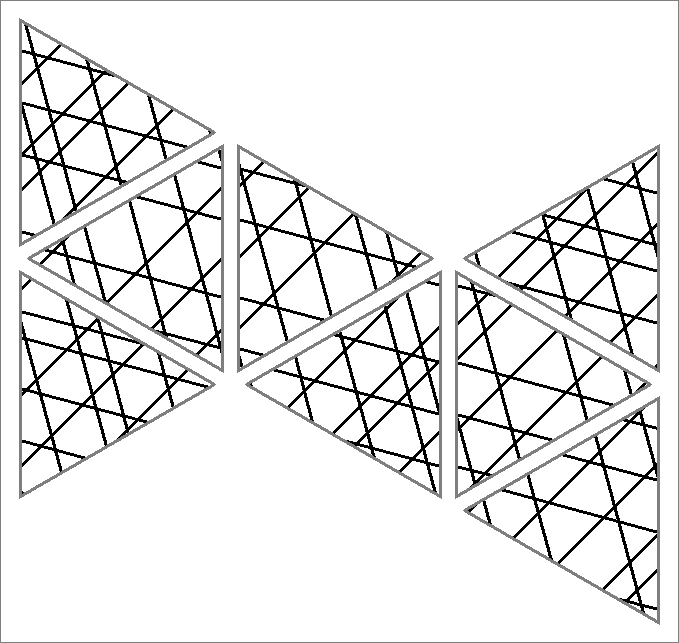 | | Contains
double edges | | |
| 180C | | 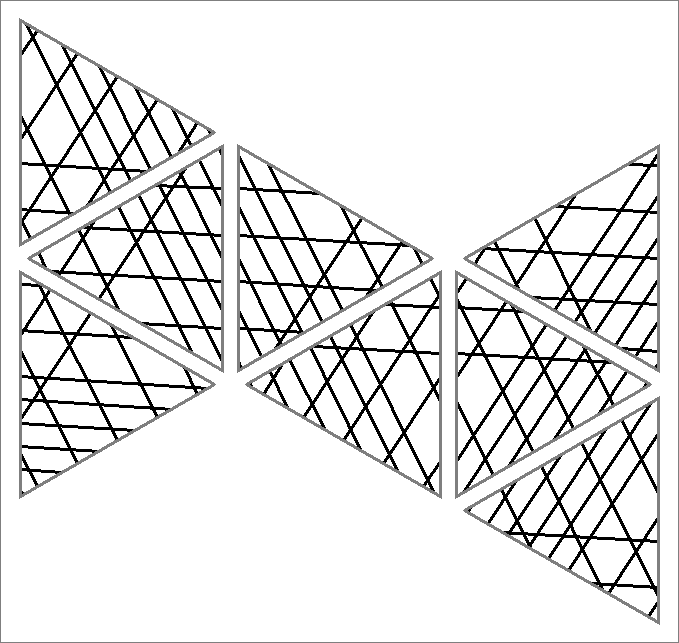 | | Contains
double edges | | |
| 180D | | 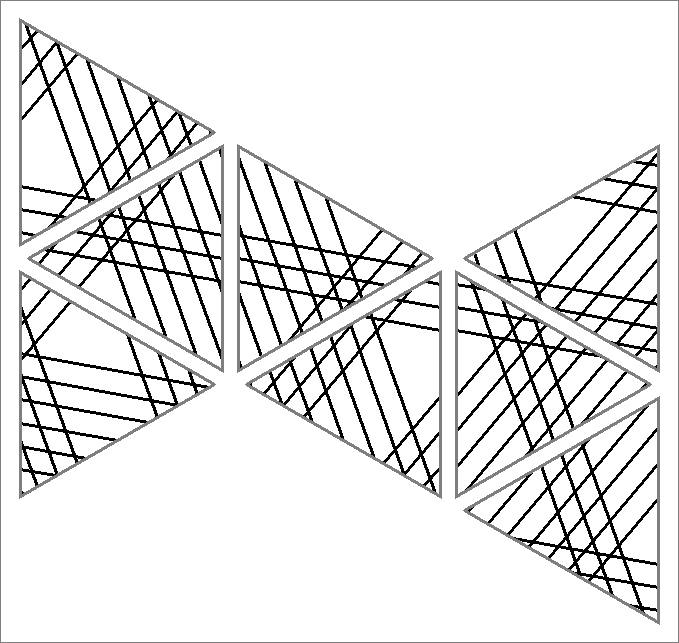 | | Contains
double edges | | |
| 180E | |  | | Contains
double edges
Same as Cube-180
and Icosahedron-180 | | 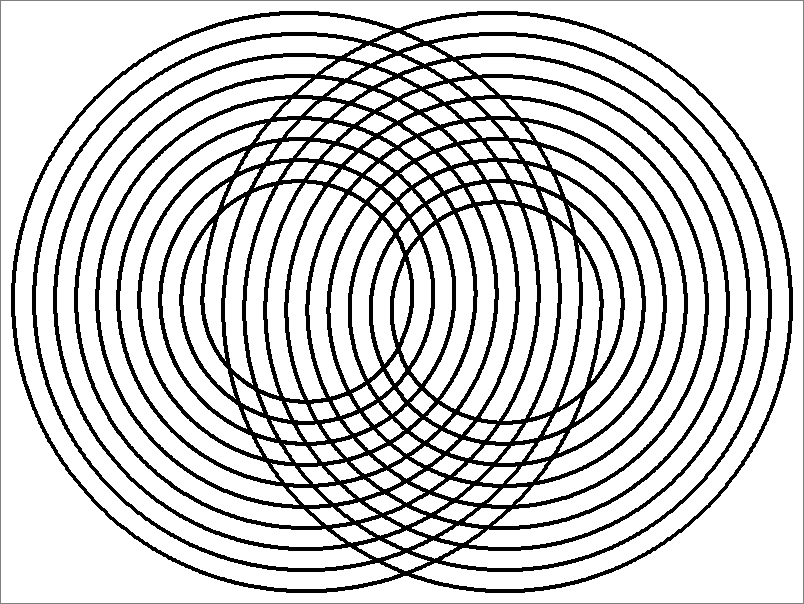 |
| 183A | | 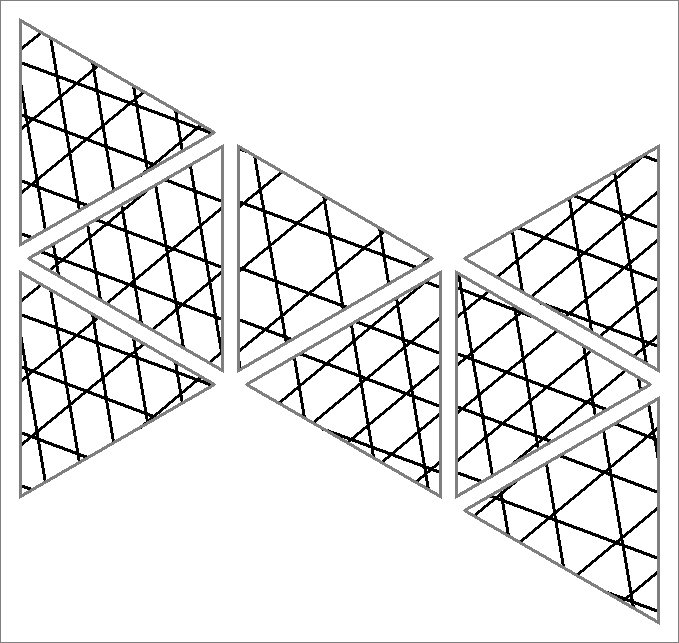 | | Contains
double edges | | |
| 183B | |  | | Contains
double edges | | |
| 187x | |  | | Contains
double edges | | |
| 189x | | 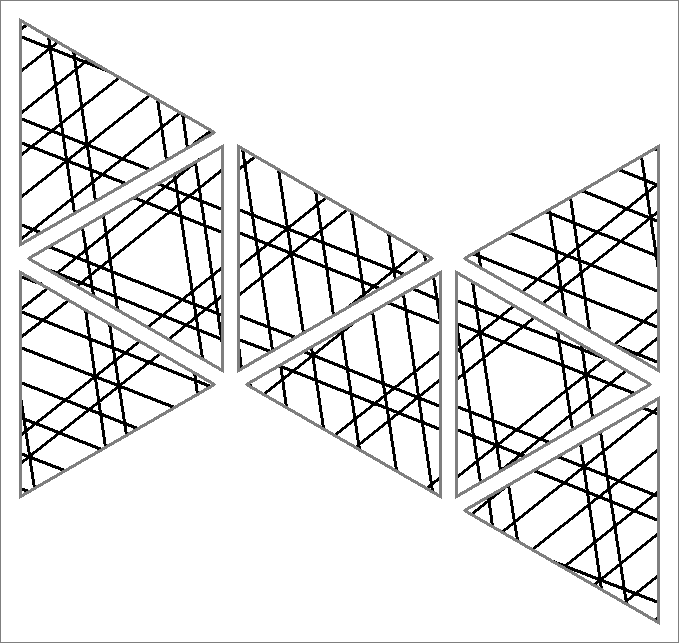 | | | | |
| 192A | | 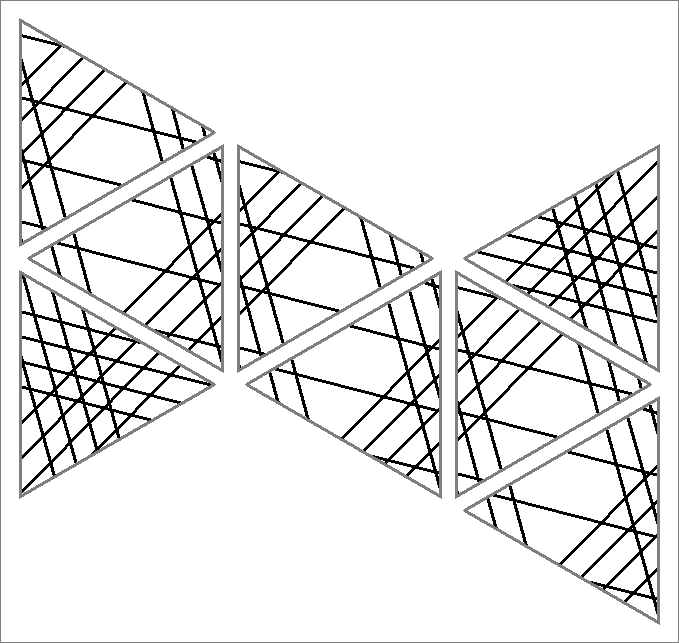 | | | | |
| 192B | | 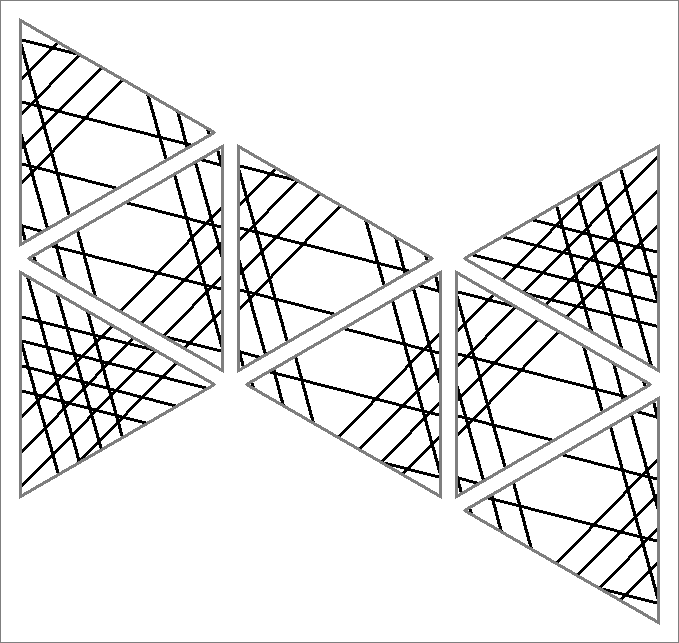 | | | | |
| 192C | |  | | Contains
double edges | | |
| 192x | | 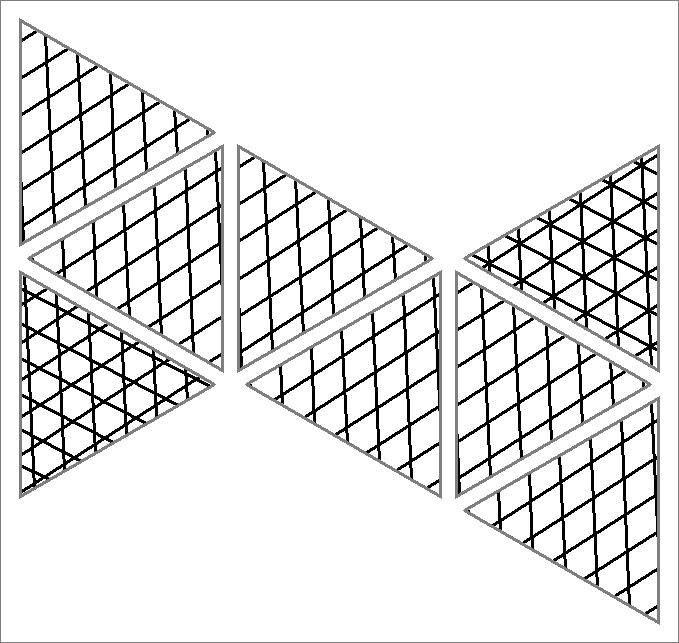 | | Contains
double edges | | |
| 198A | | 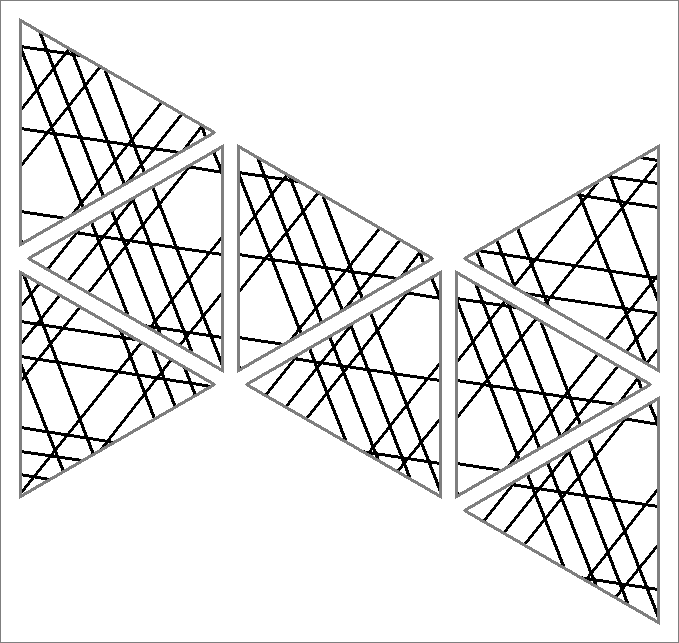 | | | | |
| 198B | |  | | | | |
| 198C | | 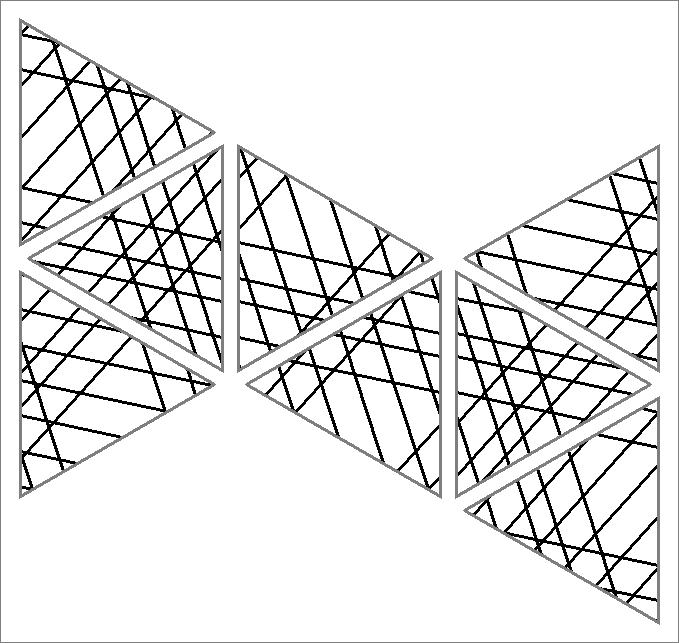 | | | | |
| 198D | | 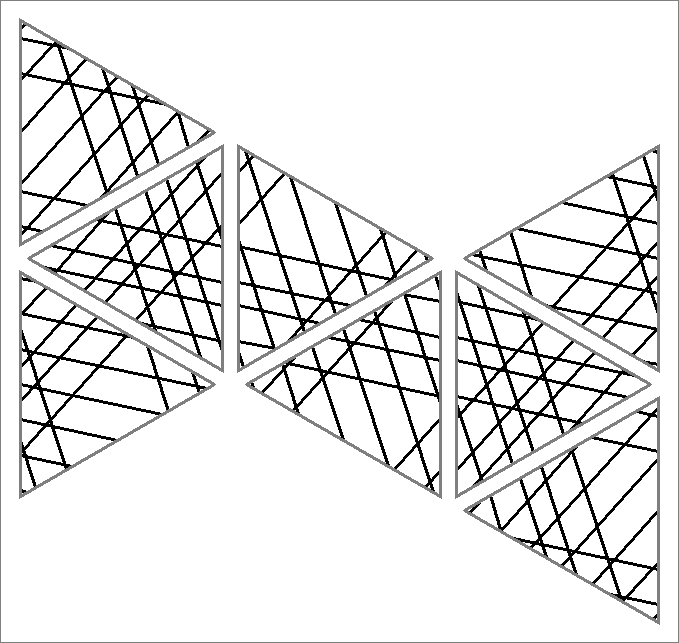 | | | | |
| 198E | |  | | | | |
| 198F | |  | | | | |
| 198G | |  | | Same as Cube-198A
and Icosahedron-198B | |  |
| 198H | |  | | | | |
| 198I | |  | | | | |










































































































































































